Triangles

Triangles are one of the most useful shapes, occurring throughout maths. There are several different types of triangles, each having its own unique properties. Some of the general features of triangles and the features for each specific type of triangle are discussed below.

General Properties of Triangles

All triangles share some of the same features, such as having three sides and the sum of their angles being \(180^{\circ}\). We can check that the angles of a triangle sum to \(180^{\circ}\) by making a triangle out of paper and then tearing the corners off, putting the corners together we should be able to see that they form a straight line, meaning they sum to \(180^{\circ}\). In our article on types of angles, we discuss how angles on a straight line always sum to \(180^{\circ}\). In the images below, we can see this process carried out.

Three images. Firstly, a right angled triangle. Secondly, the corners of the right angled triangle torn off. Finally, the torn corners arranged in a straight line.

Three images. Firstly, an isocellese triangle. Secondly, the corners of the isocellese triangle torn off. Finally, the torn corners arranged in a straight line.

Different types of triangles also have unique properties specific to them. Click on the labels to learn about the different types of triangles.

Equalateral Triangles

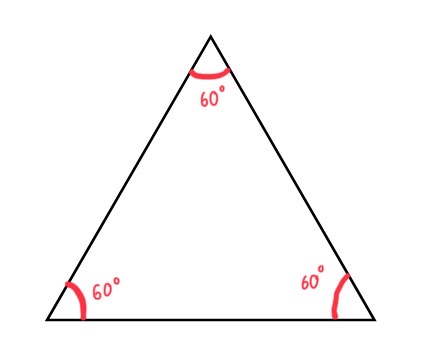
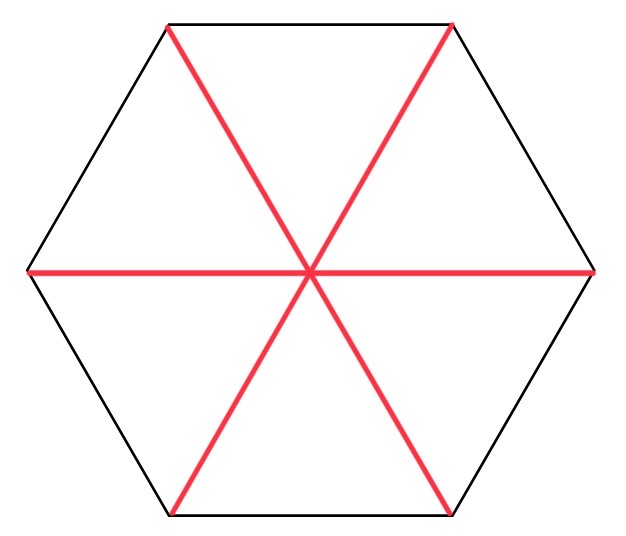
Equilateral triangles are a special type of triangle where all the sides are the same length and all the angles are the same size, which is \(60^{\circ}\). If they are the same size, we can use 6 equilateral triangles to form a hexagon, as shown below.

A regular hexagon, divided into three equalateral triangles.

We can also tessellate identical equilateral triangles with each other; an example of this is shown below.

Isoscelles Triangles

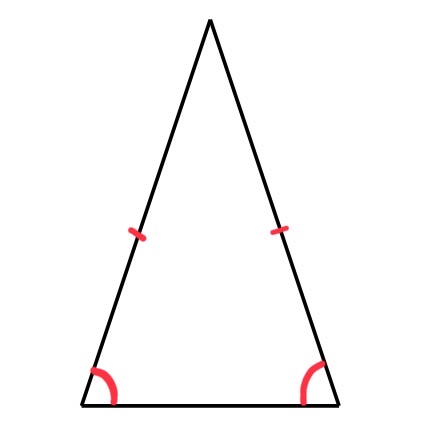
These types of triangles have two angles which are the same size and two sides which are the same length. This means that these triangles will have a line of symmetry that passes through the angle that is different from the other two.

An isoscelles triangle with a line of symmetry.

We can also tessellate identical isocellese triangles. An example of one of these tessellations is shown below.

Scalene Triangles

These types of triangles have no two angles which are the same size and no two sides which are the same length. An example of this type of triangle is shown below.

We can still tessellate identical copies of these types of triangles. An example of one of these tessellations is shown below.

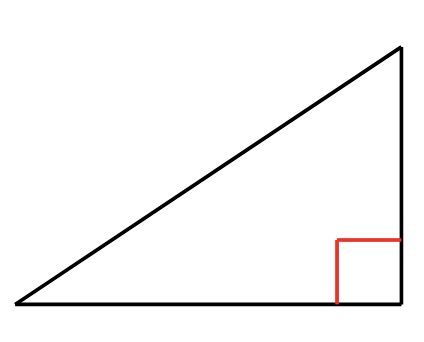
Right-Angled Triangles

These types of triangles are a special type of scalene triangle where one of the angles is a right angle. This means that the other two angles must form a right angle. You can make a right-angled paper triangle and use the tearing method again to show this. A right-angled triangle can also be an isosceles triangle if the other two angles are equal (this would mean they are both \(45^{\circ}\)).

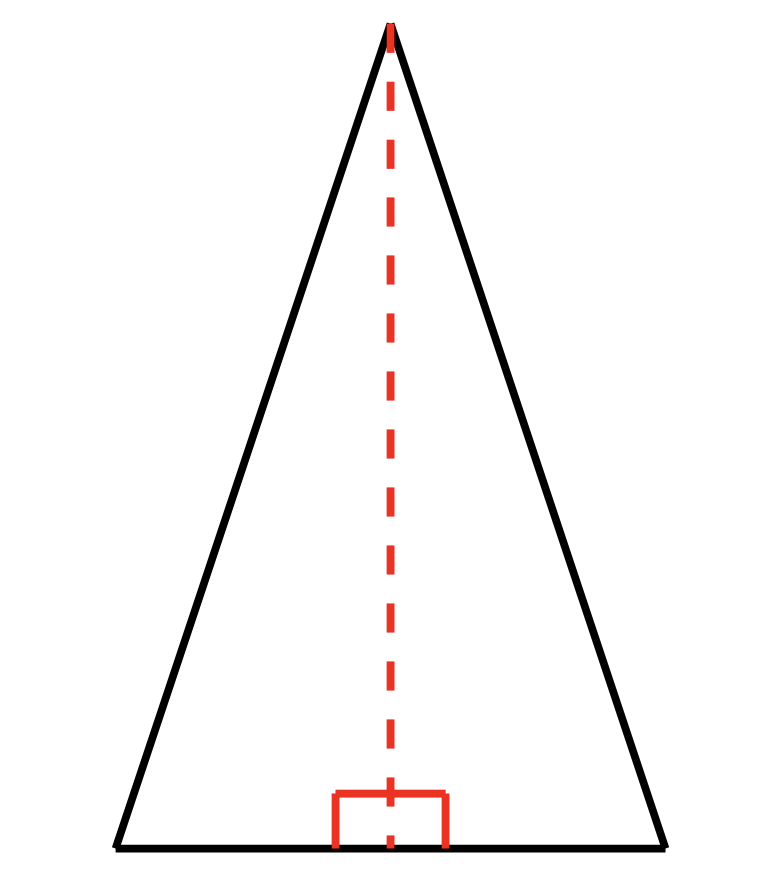
The Pythagorean theorem and trigonometry are both used on right-angled triangles, making it easier for us to determine the side lengths and angles of these triangles. This is especially helpful as we can split any non-right-angled triangle into two right-angled triangles by “dropping a perpendicular”. This means we draw a straight line from one corner of a triangle so that it meets the opposite side at a right angle. A demonstration of this is shown in the image below.

An isocellese triangle with a perpendicular line drawn from the top (the non-matching angle) down the line of symmetry.

A tesselation of right-angled triangles.

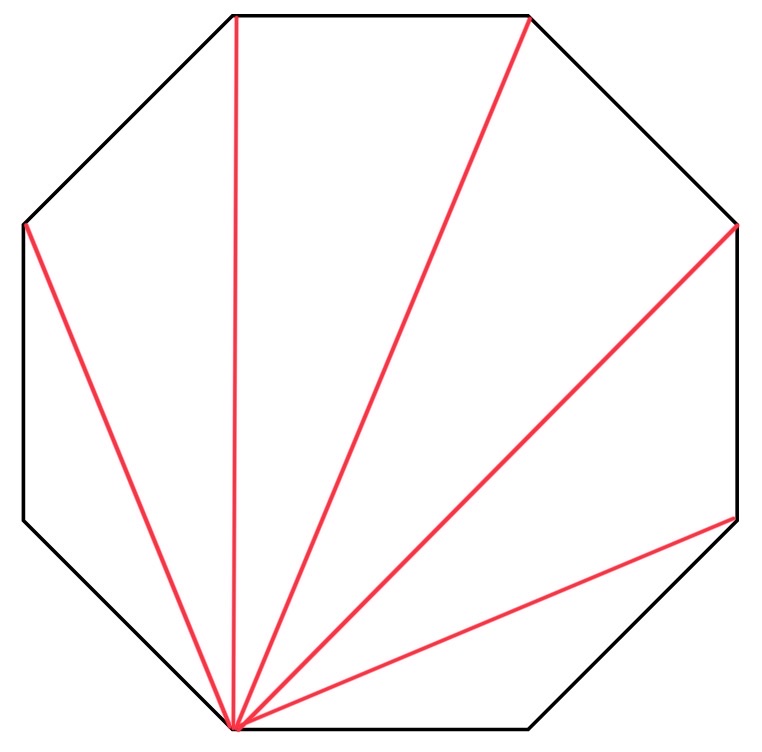
Drawing Triangles in Polygons

All polygons can be represented as triangles; this is called polygon triangulation. One way to do this in regular polygons is to choose one corner and join it to all the other corners of the polygon; this is shown in the image below.

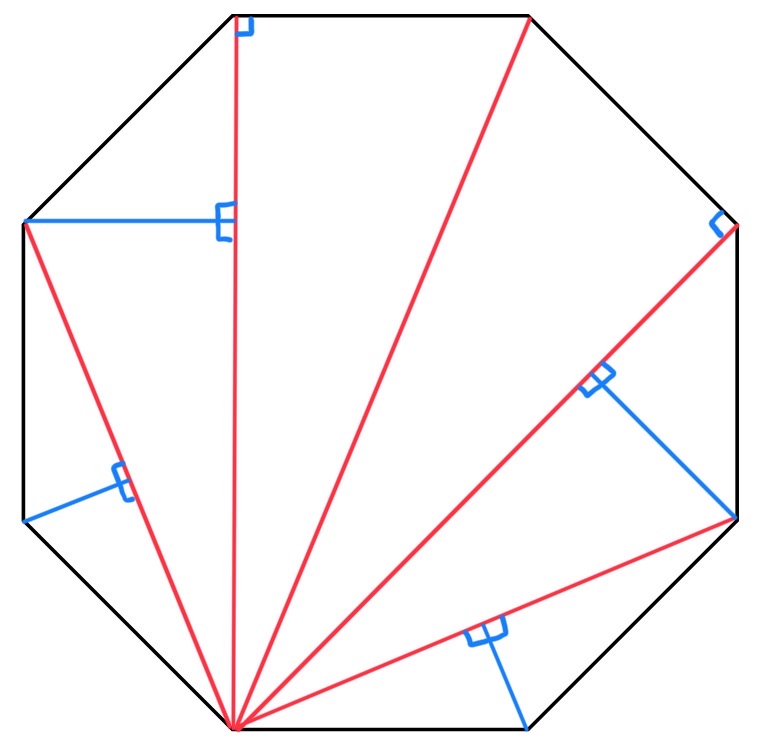
As every triangle can be split into a right-angled triangle, we can also split every polygon into a set of right-angled triangles; this is shown in the image below. Children could experiment with making their own polygons and then splitting them into triangles. If they cut these pieces out, they would get a sort of polygon puzzle where they could construct different polygons using these triangles.

Spliting a polygon into right-angled triangles.

In the image below, a child experimented with making a square using two right-angled triangles.

A child putting two triangles together to get a square

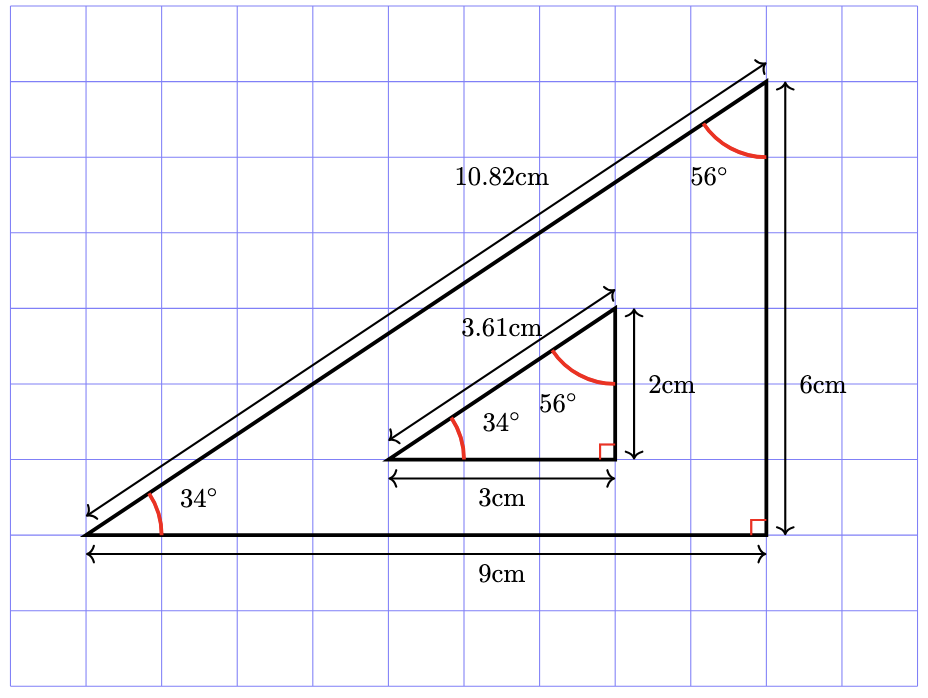
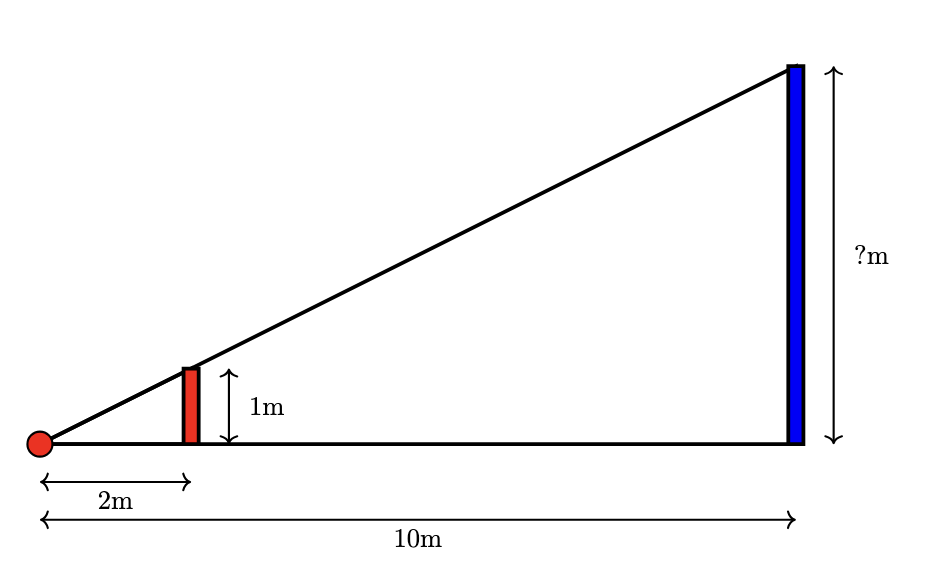
Scaling triangles

When we scale the size of a shape up or down, we keep the same angles but change the side lengths. This means that each side of a triangle will have to increase by the same factor (not the same amount) when we scale up the size of a triangle.

This means that the ratio of the side lengths in the smaller triangle and the larger triangle will remain the same. The factor the sides increase by will also be the same between each corresponding side in the two different triangles. This is illustrated in the image and table below. This relationship between similar triangles is used for perspective calculations to help us work out the height of tall objects, which would otherwise be difficult to measure.

A smaller triangle inside a larger triangle on a grid. Both triangles have angles of the same size, which are labelled. The side lengths of the triangles are given on the diagram and in the corresponding table below.

In the image above, the corresponding side lengths in the larger triangle are three times the length of those in the smaller triangle. The angles in each case remain unchanged, and the ratios between the sides of the triangle remain unchanged.