Types of Angles

An angle is a measure of the difference in the direction of two lines. They can be seen all around us, and understanding them can help us do many different things, such as navigate and build structures. In this article, we will measure angles in degrees; however, radians can also be used. Here we consider some special types of angles. For an overview of angles, please see our article on angles.

Acute Angles

Acute angles are less than \(90\) degrees. An example of an acute angle is shown in the image below.

An angle of 63 degrees on a grid.

Right Angles

Right angles are exactly \(90\) degrees. These angles are used throughout maths, especially in trigonometry, the area of maths where we calculate the angles and side lengths of triangles. When two lines make a right angle, they are called perpendicular. To learn more about this, see our article on perpendicular lines. An example of a right angle is shown in the image below.

A right angle on a grid.

Obtuse Angles

Obtuse angles are greater than \(90\) degrees and less than \(180\) degrees. An example of one of these angles is shown in the image below.

An angle of 117 degrees on a grid.

Straight Angles

A straight angle is exactly \(180\) degrees and so makes a straight line. An example of a straight angle is given below.

An angle of 180 degrees on a grid.

Normally, we don’t come across this type of angle on its own. We do, however, frequently use the fact that angles on a straight line sum to \(180\) degrees. We can see an example of this in the image below.

Five angles on a straight line on a grid. The angles are of sizes 56.3, 33.7, 18.4,37.9 and 33.7 degrees from right to left.

The angles on this line are \(56.3\), \(33.7\), \(18.4\), \(37.9\) and \(33.7\) degrees. The sum of these angles is \(180\) degrees, as expected.

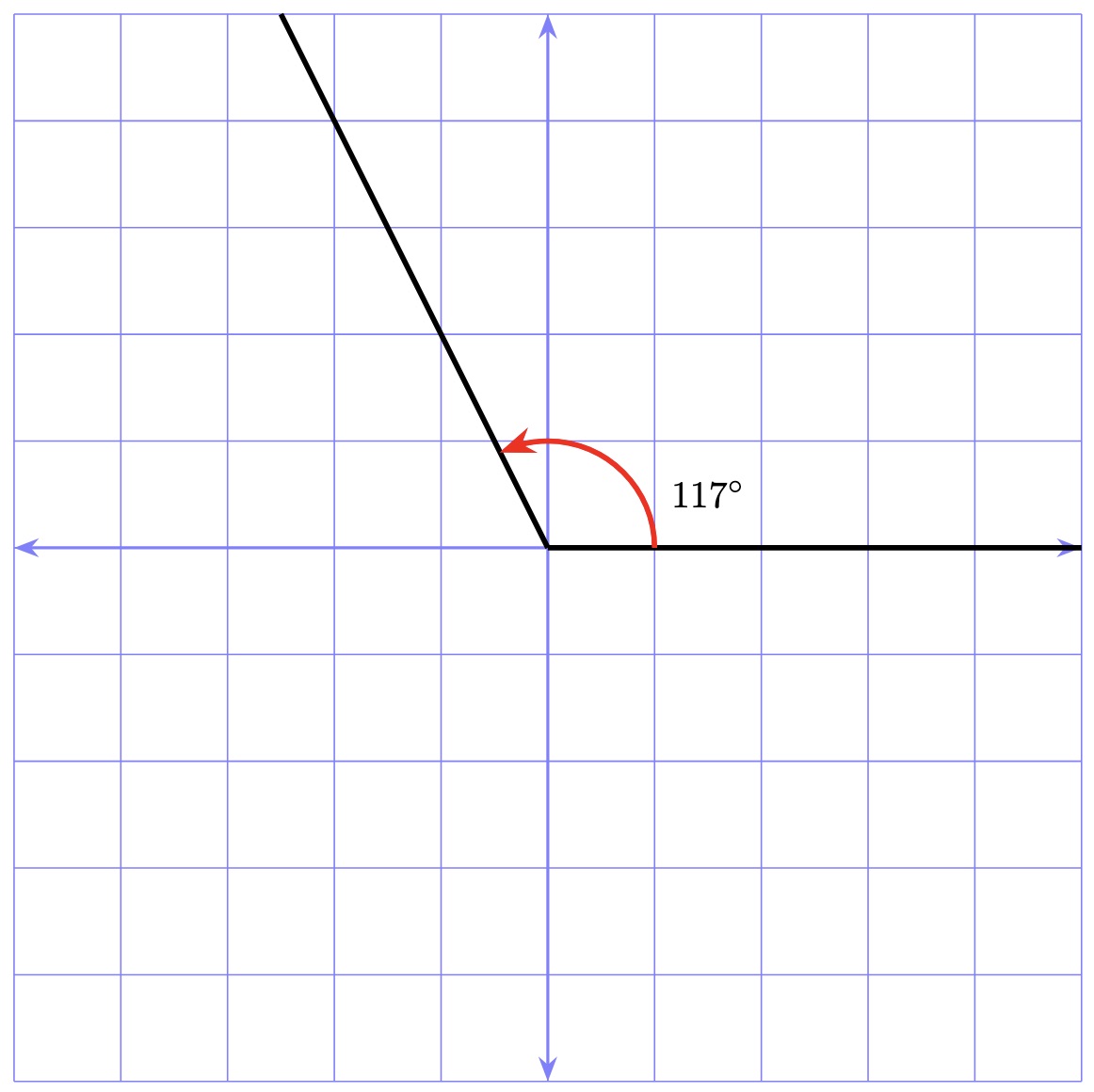
Reflex

Reflex angles are more than \(180\) degrees and less than \(360\) degrees. An example of a reflex angle can be seen in the image below.

An angle of 243 degrees on a grid.

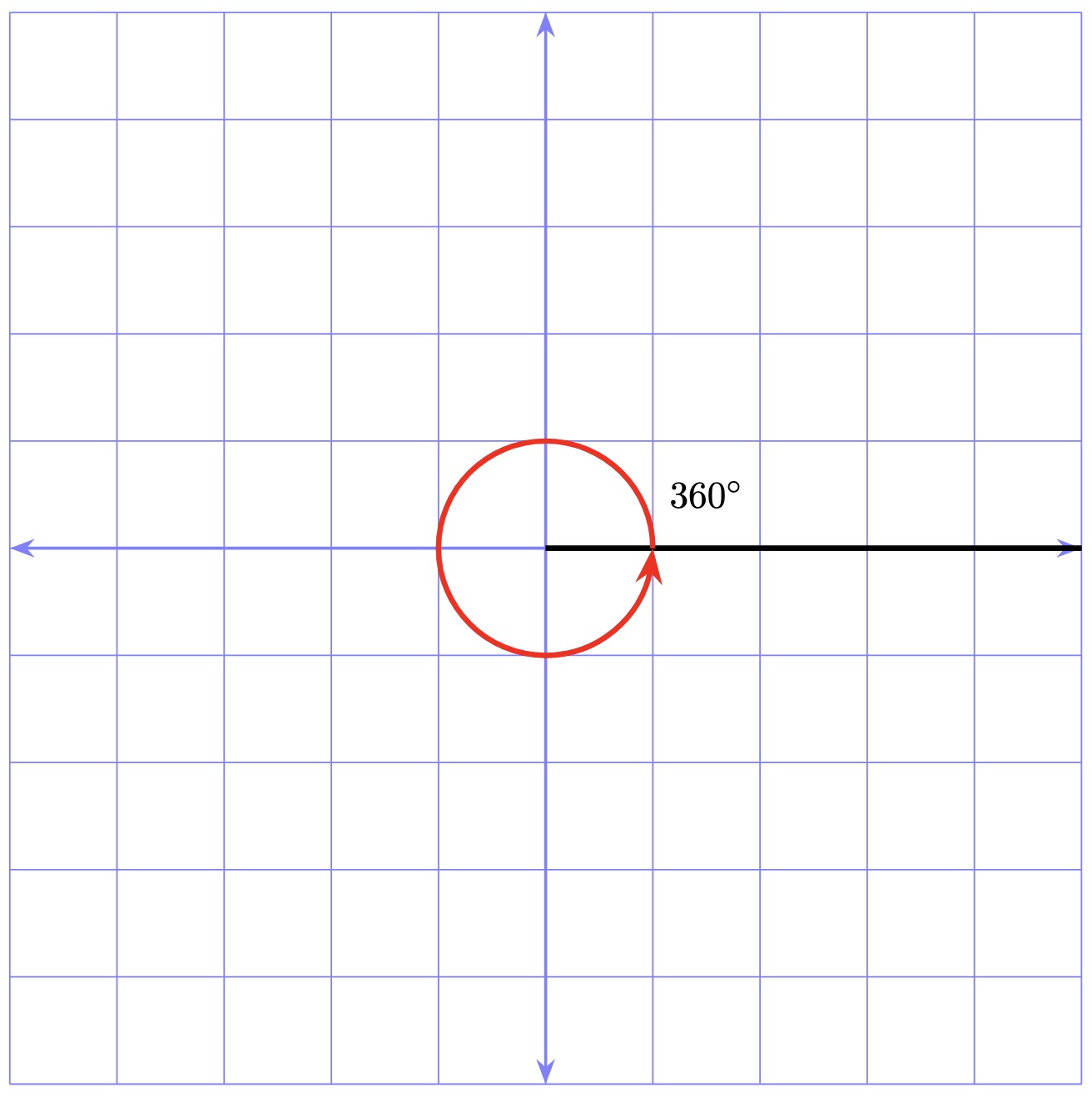
Full Circle

A full circle is \(360\) degrees. An example of the full circle is shown in the image below.

An angle of 360 degrees on a grid.

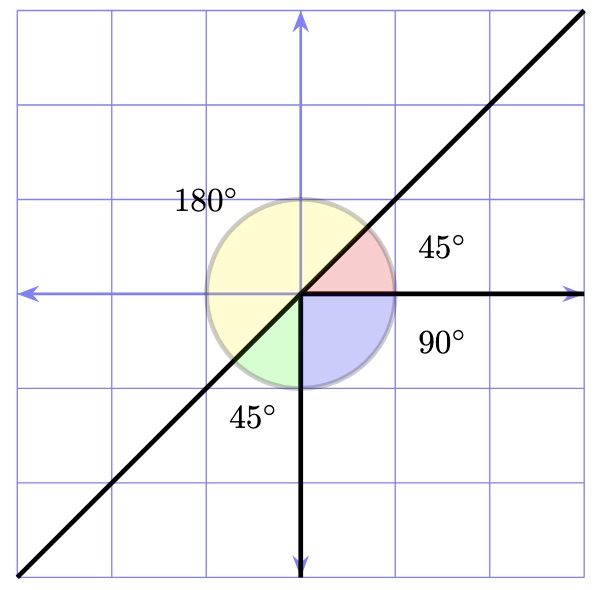
Similar to the straight line angle, we make use of the fact that angles forming a full circle sum to \(360\) degrees. An example of angles forming a circle summing to \(360\) degrees is shown in the image below.

Four angles forming a circle on a grid. The angles are of sizes 45, 180, 45 and 90 degrees (read anticlockwise).