Maths in Vegetables
Some children at nursery study vegetables and fruit as a topic. Here are some ways that this topic could link to mathematical concepts.
Weight and Density
At one nursery, a child spent time weighing a melon against several potatoes until the scales were balanced. They needed to use 12 potatoes to get the scales to balance, telling us that one melon weighs the same as 12 potatoes. We could write this relationship as the equation melon \(= 12\) potatoes. If we knew that each potato weighs 120g, we could work out the weight of the melon to be \(12 \times 120 = 1440\)g. Similarly, if we knew the weight of the melon to be 1440g, we could work out the weight of one potato to be \(\frac{1440}{12} = 120\)g.
The children could also spend some time thinking about densities, perhaps one cup of one vegetable weighs more than one cup of another. Here, the children would also need to consider how small the chunks of each vegetable were, in other words, how much empty space was left in each cup.
Fractals
As mentioned in our article on fractals, some vegetables such as romanesco and cauliflower have a self-similar structure like a fractal. In the image below, you can see an example of this self-similarity. Children could spend time discussing how the smaller sections of the cauliflower have the same structure as the whole cauliflower.
Concentric Circles and Spirals
Some vegetables also show other mathematical patterns that children may find interesting. As discussed in our article on concentric circles, both beetroots and carrots contain concentric circles when cut into circular slices. Children might also be able to identify a spiral pattern in romonessco.
Properties of Shapes
Sometimes the same type of vegetable can grow with different proportions, which could lead children to explore the questions, ‘Which has the largest volume?’ and ‘Is one more curved than the other?’ For example, some carrots can be short and wide, while others can be long and thin. To work out which carrot has a larger volume, the children could try submerging the carrots in water using a eureka can as discussed in our article on experiments with water. Alternatively, they could assume that both carrots have the same density and weigh them; the heavier carrot will then have a larger volume.
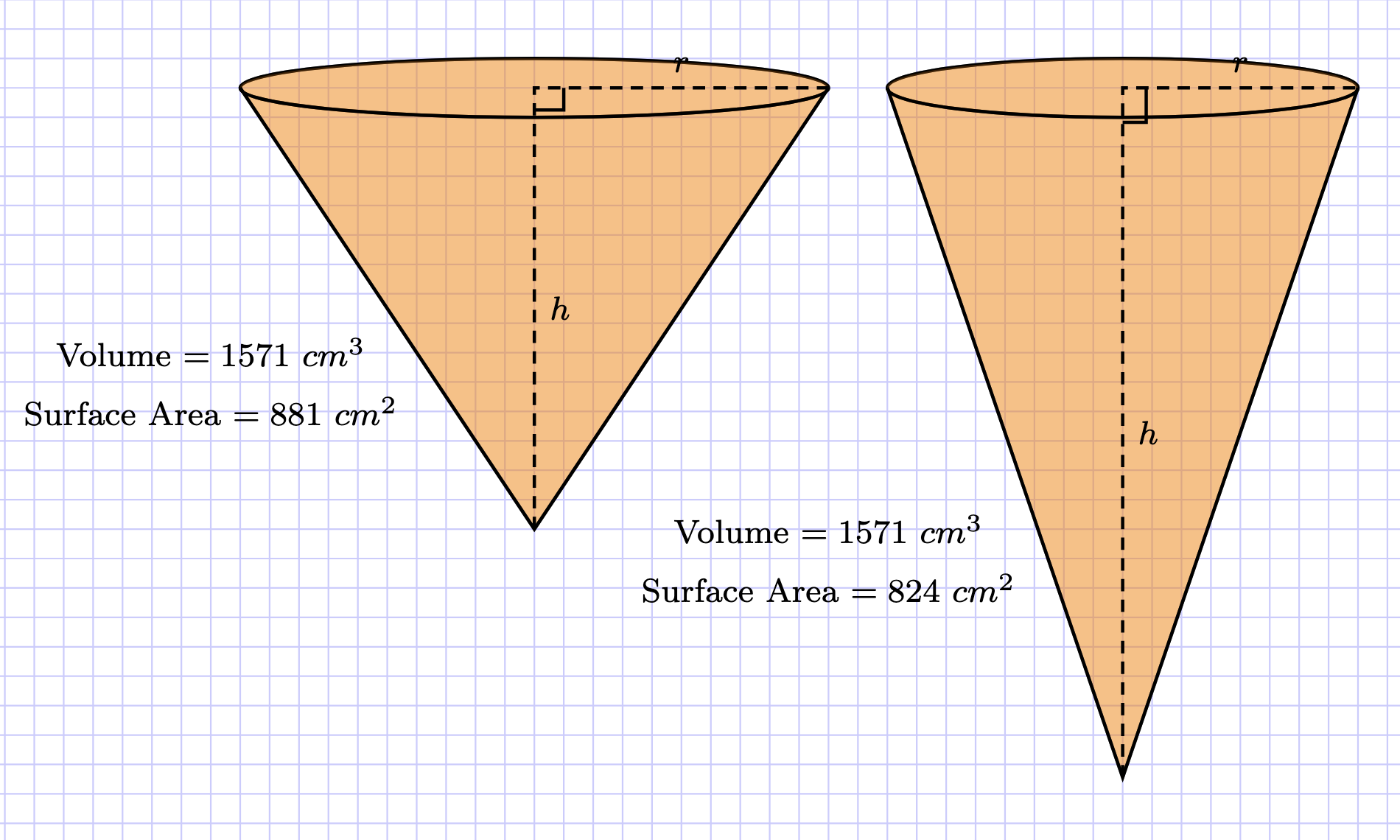
In the example below, the two carrots have the same volume but different shapes; this means that the shorter carrot has a larger surface area. Children might find it interesting to discuss why two objects can have the same volume but different areas. Would the children prefer one of the carrots over the other? Perhaps the one with a smaller surface area is desirable, as it will require less peeling and therefore result in less waste.
Click here to see the formulas used above
Here, we modelled the two carrots as cones and used the formulas for the surface area and volume of a cone.
Volume \(= \frac{1}{3} \times \pi \times h \times r^2\)
Surface Area \(= (\pi \times r^2) + (\pi \times r \times \sqrt{r^2 + h^2})\)
Here \(r\) stands for the radius of the cone, which is the same as the radius of the circle on the end of the cone. Here \(h\) stands for the height of the cone, which is shown with the radius in the diagram above.
The two carrots have different radii and heights; a summary of these is shown in the table below.
| Cone | Radius | Height | Volume | Surface Area |
|---|---|---|---|---|
| Cone 1 | \(10cm\) | \(15cm\) | \(1571cm^3\) | \(881cm^2\) |
| Cone 2 | \(8cm\) | \(23.44cm\) | \(1571cm^3\) | \(824cm^2\) |
Children might also find it interesting to consider other properties of vegetables, such as their curvature. Some carrots may bend more than others, and some potatoes may look more like spheres than others.
Fractions
Some fruits can lend themselves to a discussion on fractions. Oranges are made of many segments, and these can be counted and then shared out among the children. Given the number of segments and the number of children, we may ask if there is a way for the orange to be shared equally.
Lines of Symmetry
Vegetables can be cut in different ways. Children might find it interesting to think about whether the vegetable has any lines of symmetry and, if so, how they could cut the vegetable along this line of symmetry.