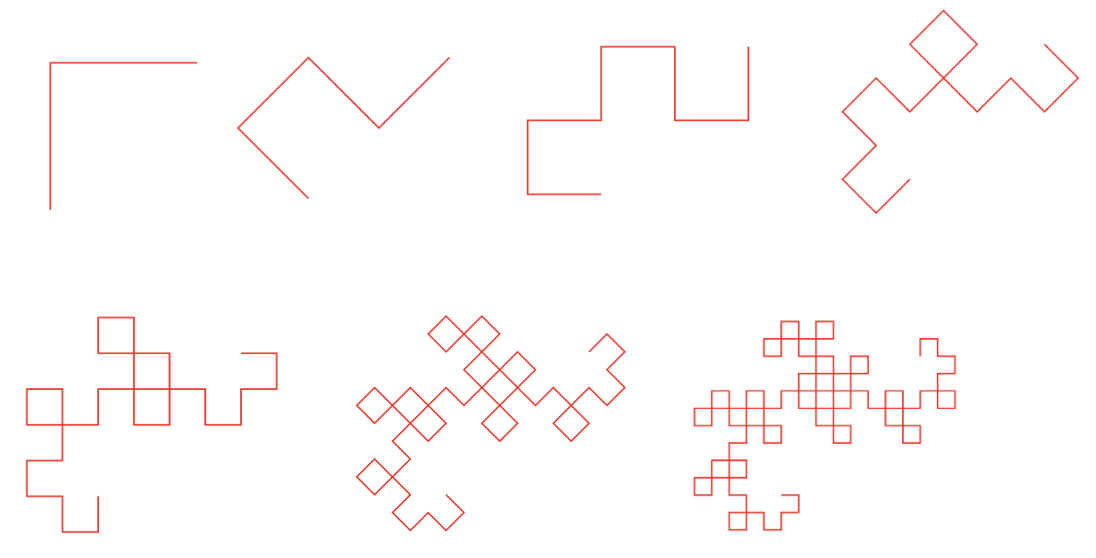Fractals

A group of the children were analysing cauliflower and noticed that the smaller parts of the cauliflower that we are able to remove from it, are much like the larger branch of cauliflower, just much smaller. This is a great example of fractals, which are “infinite patterns in which that each section of the pattern is almost identical to the pattern as a whole”.

T: It’s littler
L: And that’s bigger, bigger!
R: The same and not the same!
M: It’s big and little
L: It looks the same and doesn’t look the same
T: This is a littler one of the big one

The children pick up on the fact the same structure is repeated over and over again: the whole head of cauliflower looks the same as a floret that has been broken off, and a smaller mini-floret broken off that one is like a miniature whole cauliflower.

The practitioner takes this opportunity to introduce the new word fractal to the group

At this point I explained the new word ‘fractal’ and explained its meaning to the group. L looked at me like I was mad and responded with “Fractal - what is that?!”. I explained again that the recurring pattern that we have been talking about, that we can see by looking at all the florets, is a fractal. We all said the word several times to see how it felt when we spoke it, and also clapped the two syllables of the word.

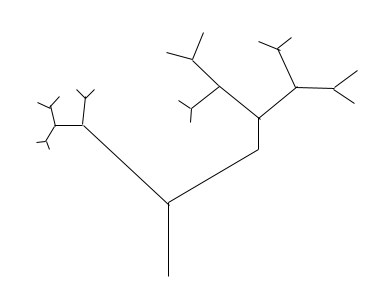
There are many other examples of fractals in nature, which we can encourage the children to think about. Broccoli has a fractal pattern, similar to cauliflower and so does romanesco (although it’s not easy to find.) There are lots of things in nature that have a fractal branching pattern, like trees, lightning or the inside of a lung.

We can look at these fractals and think about how the pattern repeats, going back to the cauliflower, having hundreds of the tiny “bumps” making up the slightly bigger “bumps” and then this repeating until you have the whole entire cauliflower. This works particularly well for trees as, they start with the large, thick trunk, which then goes into lots of connected branches. Each of these branches then have their own smaller branches, which will then have even smaller branches, repeating until the end of the tree branch. The image below visualises this in a simple way:

In nature, fractals have to stop at some point, but in maths they can go on forever. This usually happens by keeping on applying a simple rule.

• Sierpinski triangle
• Menger sponge
• Koch snowflake ~ this has an infinite perimeter, but a finite area.
• Gabriel’s horn ~ this has an infinite surface, but a finite volume.

Children might find it interesting to look at some of these patterns and even investigate the structure of some fractals for themselves. The dragon curve fractal can be made by folding a piece of paper in half multiple times. Keeping the folding direction the same (like repeatedly shutting a book) children can see the dragon curve grow. In the images below we have the first seven iterations of the dragon curve and the second, third and fourth iteration of the dragon curve made by folding a piece of paper repeatedly in half.