Triangular Numbers

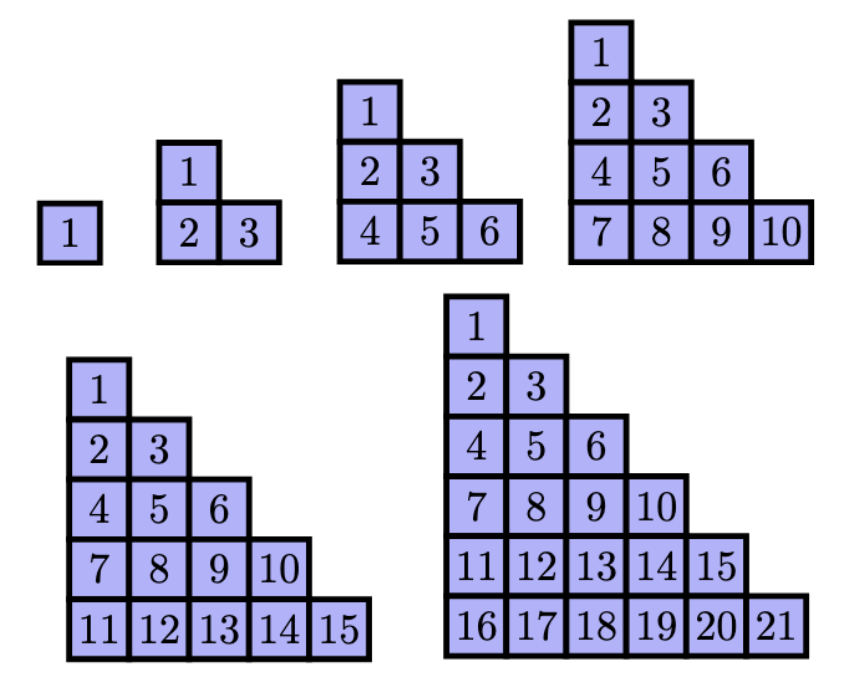
Children who are interested in learning about number sequences may enjoy working with triangular numbers. These are a sequence of numbers that increase by a larger amount each time. The sequence begins with \(1,3,6,10,15,21,...\) as shown in the image below. You may notice the difference between each number and the next increases by 1 each time.

These numbers are called triangular numbers, as we can arrange them in stacked triangles as shown below. Children could make these numbers themselves using blocks.

Handshaking and the Triangular Numbers

One useful property of the triangular numbers is that they tell us how many handshakes would need to happen for a group of people to all shake hands with each other.

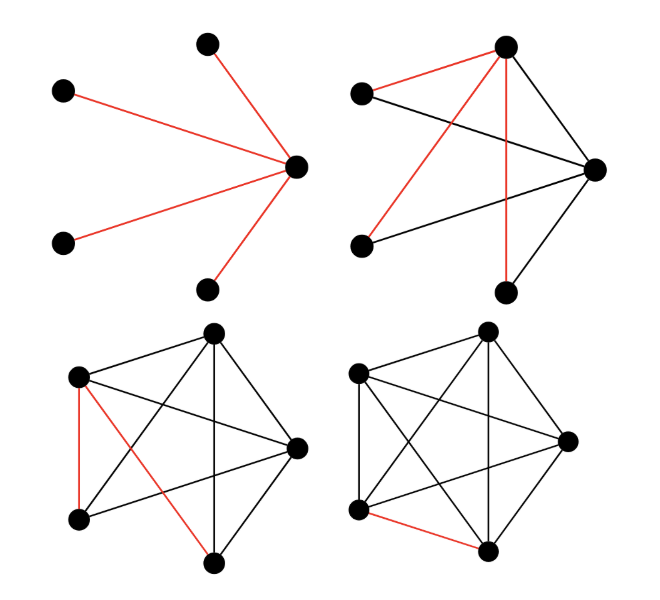
Imagine a group of 5 people. How many handshakes would happen if each person shook the hand of each other person exactly once? We could start by letting the first person shake the hand of every other person; this would take four handshakes in total. Next, the second person could shake hands with all the other people except the first person, as they have already shaken hands, this will take three handshakes in total. We can carry on in this way until everyone has shaken each other’s hand, giving in total \(4 + 3 + 2 + 1 = 10\) handshakes. We can see some graphs representing the handshakes below.

In the final graph, everyone has shaken hands with each other, so each point (node) is connected to all other nodes. When we have a graph where each node is connected to every other node exactly once, we say the graph is complete.

We might notice the total number of handshakes is 10, which is the fourth triangular number. This is because the number of handshakes needed grows as we add people to the group in the same way as the triangular numbers. For example, when we have 2 people 1 hand shake is needed, for 3 people 3 handshakes are needed, for 4 we need 6 and for 5 we need 10. The number of handshakes needed for some \(n\) people is then the \((n-1)\)th triangular number.

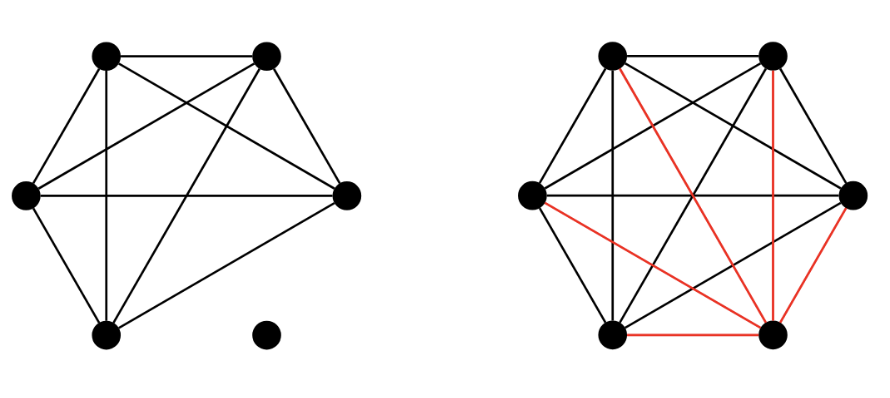
To get a better idea of how this works, we can think about what happens when we add a sixth person to the group. In the image below, we can see that 5 new lines have to be added to our graph so that the new sixth person shakes hands with each of the original 5.

When we add a new person to the group they must shake hands with every other person in the group increasing the number of handshakes by the number of people in the new group minus 1. As we add more people to the group the number of extra handshakes needed then increases with respect to the group size.

Square and Triangular Numbers

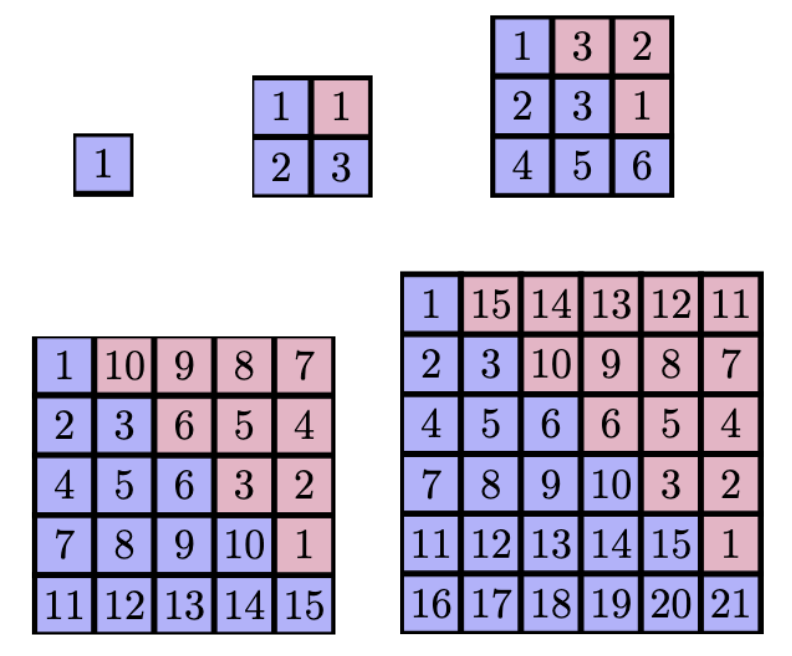
We can also make the square numbers out of consecutive triangular numbers. If we add the fifth and the fourth triangular numbers, which are 10 and 15, we get the fifth square number, 25. In the image below, we can see that the triangular formations of these numbers slot together perfectly.

To learn more about the algebra behind this click here

When we add two consecutive triangular numbers together, one is the \(n\)th triangular number with \(n\) rows and the other is the \((n-1)\)th triangular number with \((n-1)\) rows. Here \(n\) is some unknown number greater than 1. When we add the two together, the bottom row with \(n\) blocks gets no contribution from the smaller triangular number. In the next row up, we have \((n-1) + 1\) and in the next row, we have \((n-2) + 2\). This continues on until we reach the top row, where we have \(1 + (n-1)\). This means that we have in total \(n\) rows containing \(n\) blocks each. This gives \(n \times n = n^2\) blocks in total.

In the example above, we added the 5th and 4th triangular numbers together, meaning that we had 5 rows of 5 blocks, making the total number of blocks \(25 = 5^2\).

To learn about more number sequences you can read our article about the Fibonacci numbers.