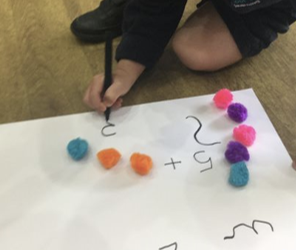The Fibonacci Numbers
One fascinating thing about nature is the occurrence of the Fibonacci numbers. The Fibonacci numbers are a sequence of numbers starting \(0,1,1,2,3,5,8,...\).
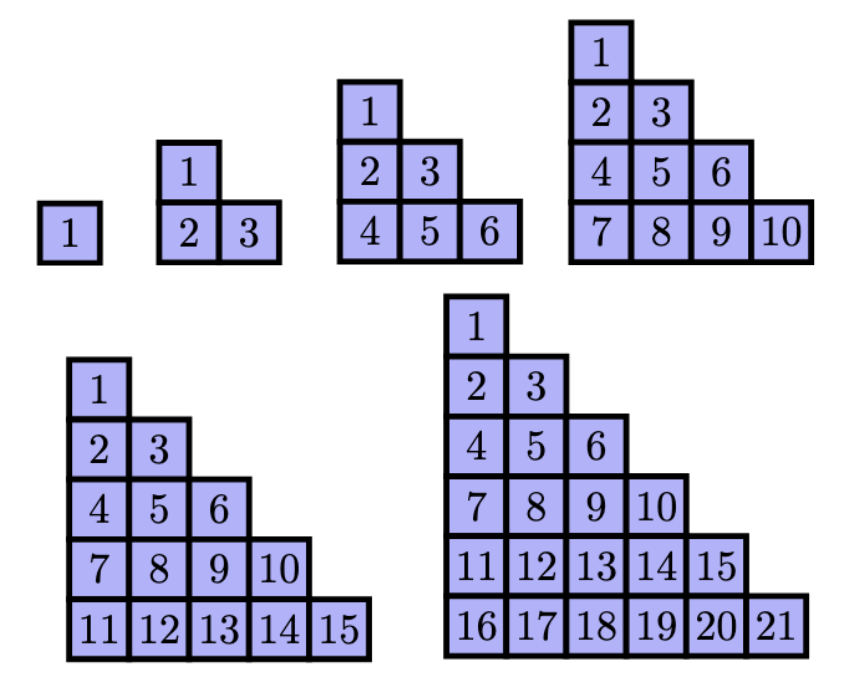
We can construct the Fibonacci numbers by first starting with \(0,1\) and then adding the last digit and the second to last digit to get the next digit. For example, to get the next digit after \(0,1\) we would add \(0\) and \(1\) to get \(1\). To get the next digit, we would add \(1\) and \(1\) to get \(2\) and so on.
The first \(20\) Fibonacci numbers are: \(0,1,1,2,3,5,8,13,21,34,55,89,144, 233, 377, 610, 987, 1597, 2584\) and \(4181\). These numbers are a good example of the use of a repeated mathematical rule, and they also occur in nature, making them interesting to talk about with children. In the images below, we can see how children have explored the Fibonacci numbers using different coloured pompoms. Some of the comments made by the children are given below:
“I can do adds, I can write them numbers and it makes the sum. The balls mean you add them together.”
“This number 8 is like a snowman. My have 8 balls cos that 5 and that 3 makes that 8”
“These sums equal and then you add them onto the next one”
“2 and 1 is 3”
“These sums equal and then you add them onto the next one”
The Fibonacci numbers can also be found in plants. When we look at plants with visible seeds, these seeds are often arranged in spirals, and the number of spirals is often a Fibonacci number. Spirals can be seen in two directions on plants, and the number of spirals in one direction is often a consecutive (next in the sequence) Fibonacci number to the number of spirals in the other direction.
In the image below we can see children exploring the spirals in pinecones.
In the image below, we can see that the sunflower has \(21\) spirals in one direction and \(34\) spirals in the opposite direction, which are consecutive Fibonacci numbers. The sunflower uses relatively large Fibonacci numbers, but spirals occurring in smaller Fibonacci numbers can be found elsewhere in nature, for example, in pinecones. Children could try to count the spirals in pinecones using tape to make the spirals easier to see.
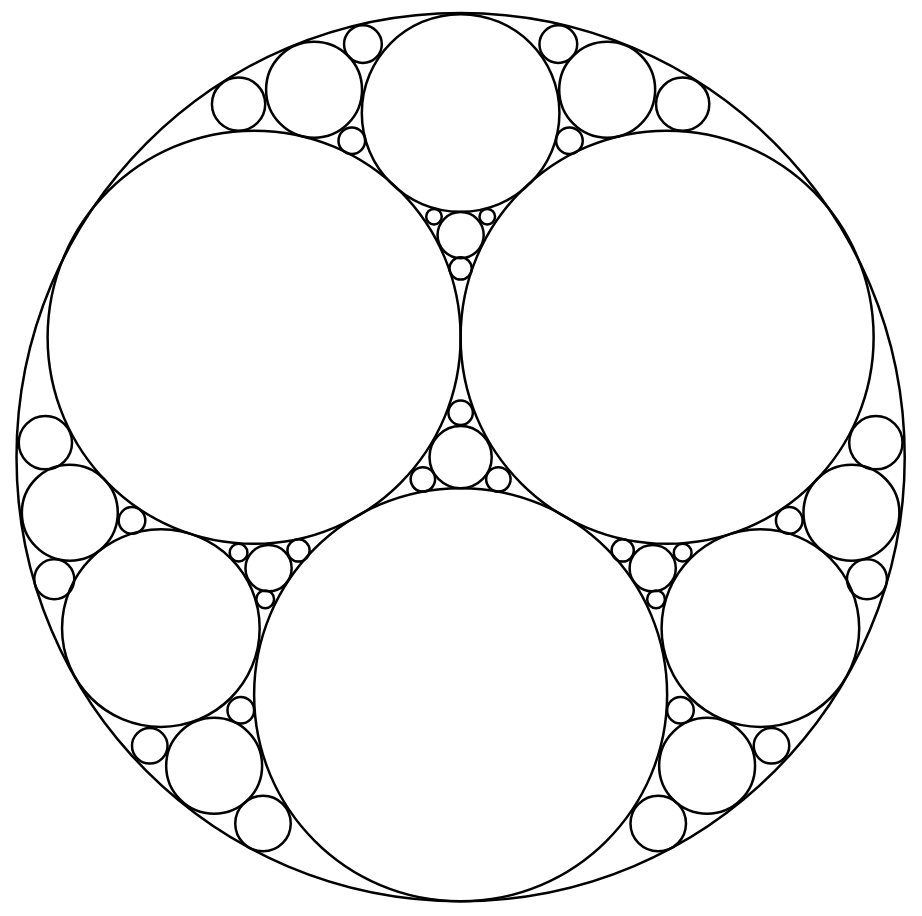
The Fibonacci numbers can also be used to construct the golden spiral. The golden spiral can be seen throughout nature, in snail shells, for example. The Fibonacci numbers can be used to construct an approximation of the golden spiral as they approximate an important number called the golden ratio. The golden ratio \(1.618033…\) is used throughout mathematics but also in other areas such as art and architecture. The golden ratio can be approximated by the Fibonacci numbers by taking one number in the sequence and dividing it by the previous number in the sequence. As the Fibonacci numbers become larger, this number becomes closer to the golden ratio, as we see in the table below.
| Fraction of two subsequent Fibonacci numbers | Outcome |
|---|---|
| \(\frac{1}{1}\) | 1 |
| \(\frac{2}{1}\) | 2 |
| \(\frac{3}{2}\) | 1.500000 |
| \(\frac{5}{3}\) | 1.666667 |
| \(\frac{8}{5}\) | 1.600000 |
| \(\frac{13}{8}\) | 1.625000 |
| \(\frac{21}{13}\) | 1.615385 |
| \(\frac{34}{21}\) | 1.619048 |
| \(\frac{55}{34}\) | 1.617647 |
| \(\frac{89}{55}\) | 1.618182 |
| \(\frac{144}{89}\) | 1.617978 |
| \(\frac{233}{144}\) | 1.618056 |
| \(\frac{377}{233}\) | 1.618026 |
| \(\frac{610}{377}\) | 1.618037 |
An approximation of the golden spiral can be seen below. If you haven’t already, check out our article on spirals to learn more about the golden spiral.