Shapes in Shapes

Many children like drawing different shapes, and there can be some entertaining drawing tasks that they can do by drawing shapes in shapes.

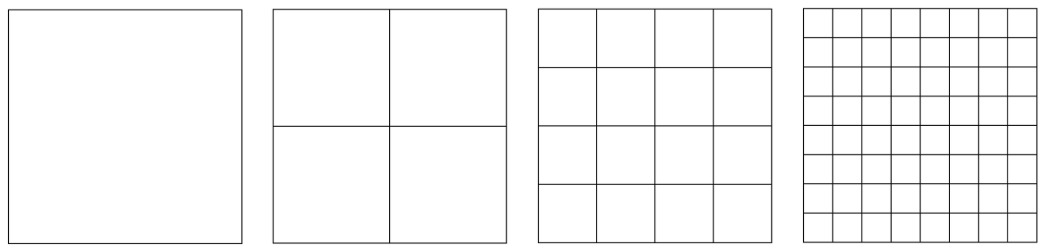
Squares in Squares

A simple drawing task could be for children to continue to split a square into smaller and smaller squares; in each case, a square will contain four of the smaller squares. This is shown in the illustration below. We start with 1 square, which is then split into 4 and then 16 and then 64. Each time we multiply the number of squares by 4, as each existing square is split into 4.

If we continued to segment the squares forever, this drawing would become self-similar and a fractal, as seen below.

Filling shapes with triangles

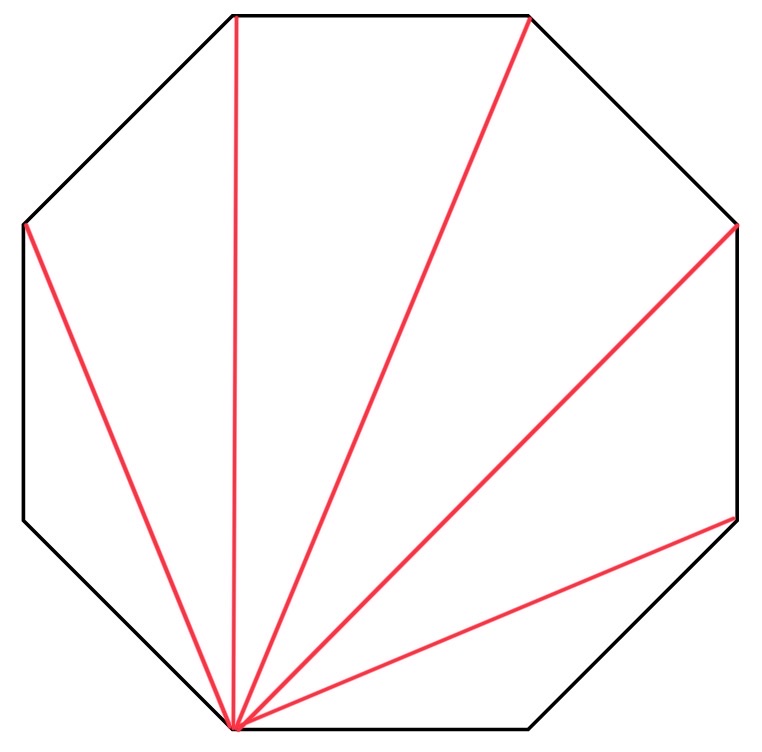
Children could also try a similar game, filling shapes with triangles. If the starting shape is a polygon, they should be able to completely fill the shape with triangles as shown below. If the shape is curved, increasingly smaller triangles will need to be used; this will take infinitely many triangles.

In the image below, the octagon has been split into six triangles.

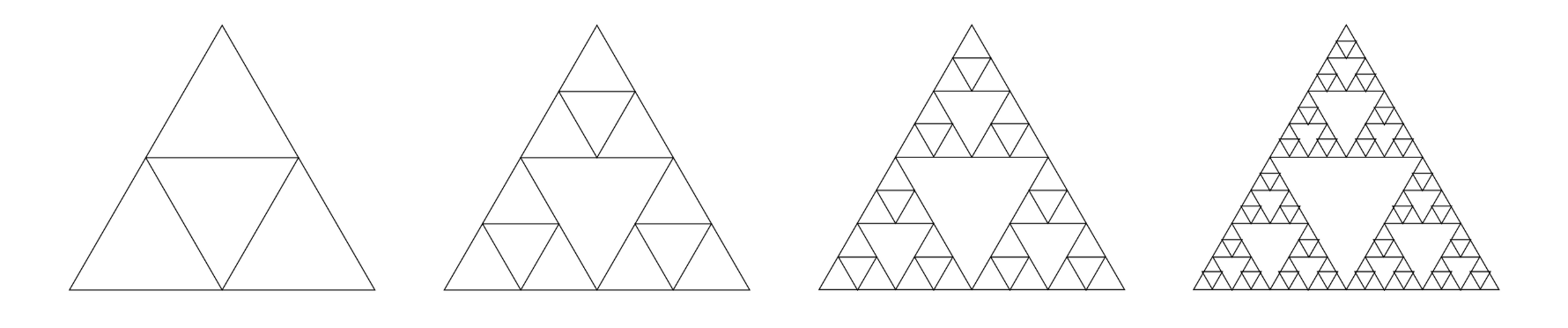
Triangles in Triangles

One special case of this is to use equilateral triangles within an equilateral triangle. Starting with one ‘upright’ equilateral triangle, children could try to fill in the space inside with the largest ‘upside down’ equilateral triangles possible. A demonstration of this is shown below; continuing this process infinitely gives the fractal known as the Sierpiński triangle.

Below is a further iteration of the Sierpiński triangle, where more stages of space-filling have been carried out.

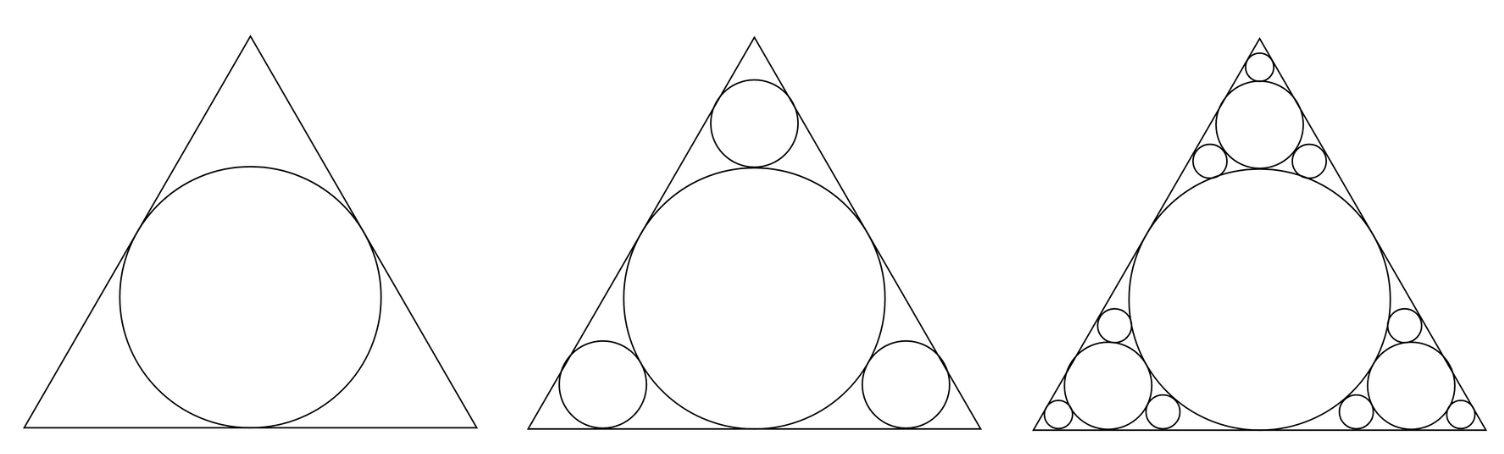
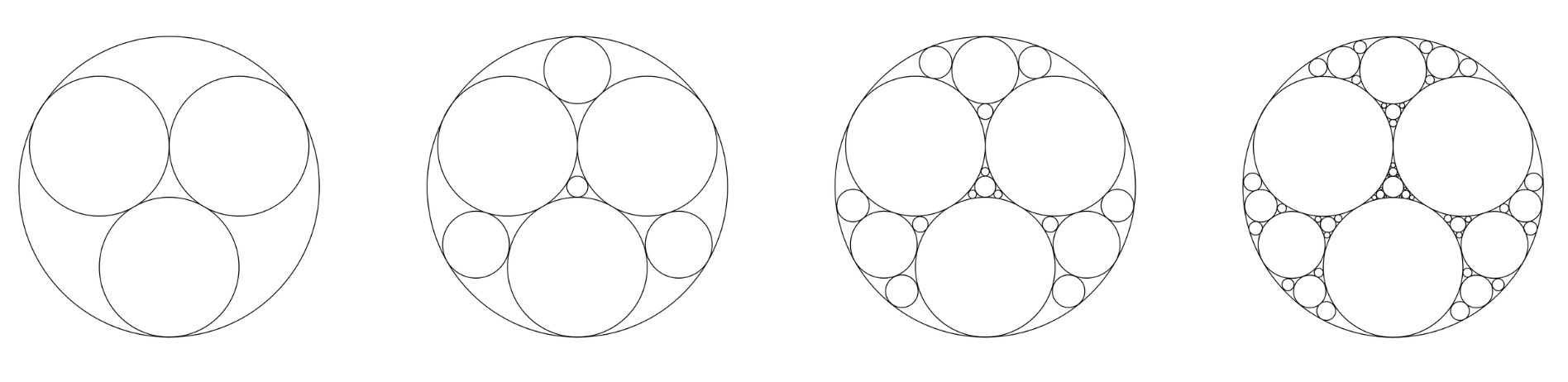
Filling Shapes with Circles

Children could also try filling different shapes with circles; as circles do not tessellate with each other, there will be gaps left that can be filled with smaller and smaller circles. This process could carry on forever if we were able to draw infinitely small circles. Some special examples of this are called Apollonian gaskets.

In the image below, we have begun with an equilateral triangle and then drawn the largest circle possible inside the empty space left in the triangle at each stage.

In the image below, we have begun to construct an Apollonian gasket, beginning with three equal circles inside one larger one. The remaining space has then been filled with smaller and smaller circles. There are different types of Apollonian gaskets; this one is satisfyingly symmetrical.