Pi

Pi (\(\pi\)) is an irrational number that is very important in maths, especially in the maths of circles.

An irrational number is a number that cannot be neatly expressed as a fraction; this means that it goes on forever. This means that \(\pi\) has an infinite number of digits.

In maths \(\pi\) is a very important number because of its links to circles. Both the circumference and the area of a circle are calculated using \(\pi\); the equations for this are given below.

\begin{equation} \text{area }= \text{ radius}^{2}\times \pi \end{equation}

\begin{equation} \text{circumference }= 2\times\text{ radius}\times \pi \end{equation}

If you want to know more about the radius of a circle, please see our article on circles.

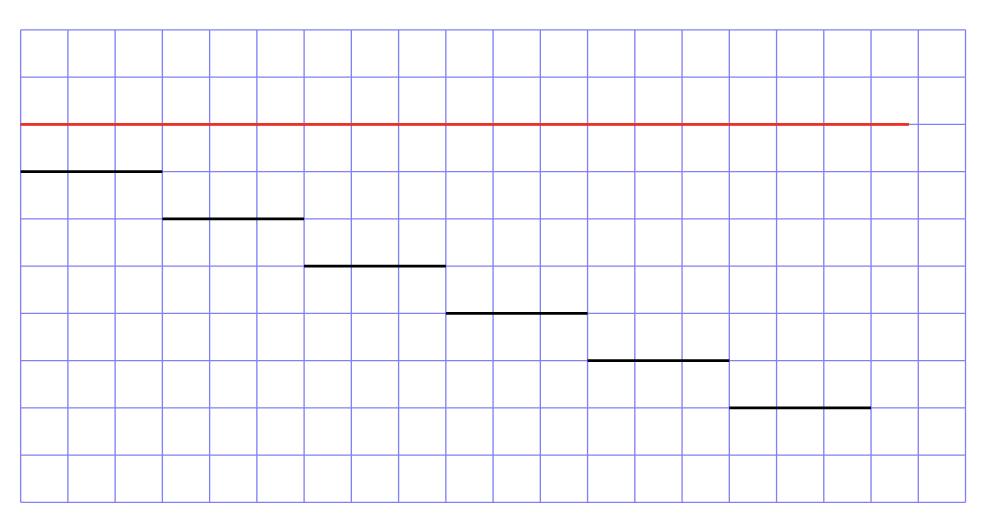
From the first equation, we can learn that \(2\times \pi\) is the number of measurements of the radius that are needed to make the circumference of a given circle. This tells us that pi is a ratio between the size of the radius and the size of the circumference of a circle. This means that the circumference of a circle is \(2\times3.14… = 6.28…\) times larger than the radius of that circle. This can be visualised in the image below. The red line is the length of the circumference, and the black lines are each the length of the radius of a circle. We can see that \(6\) lengths of the radius are nearly as long as the circumference.

Straight lines on a grid. There is one red straight line at the top, which is the length of the circumference of a circle with a radius of three. Below, on separate lines, are six black lines representing the length of the radius. The start of one line is in line with the end of the previous line.

Children could explore the ratio between the radius of a circle and the circumference by wrapping pieces of string the same length as the radius of a circle around the outside of the circle. They should find that they need just more than \(6\) for each different circle, and that this is the same no matter what size the circle is.

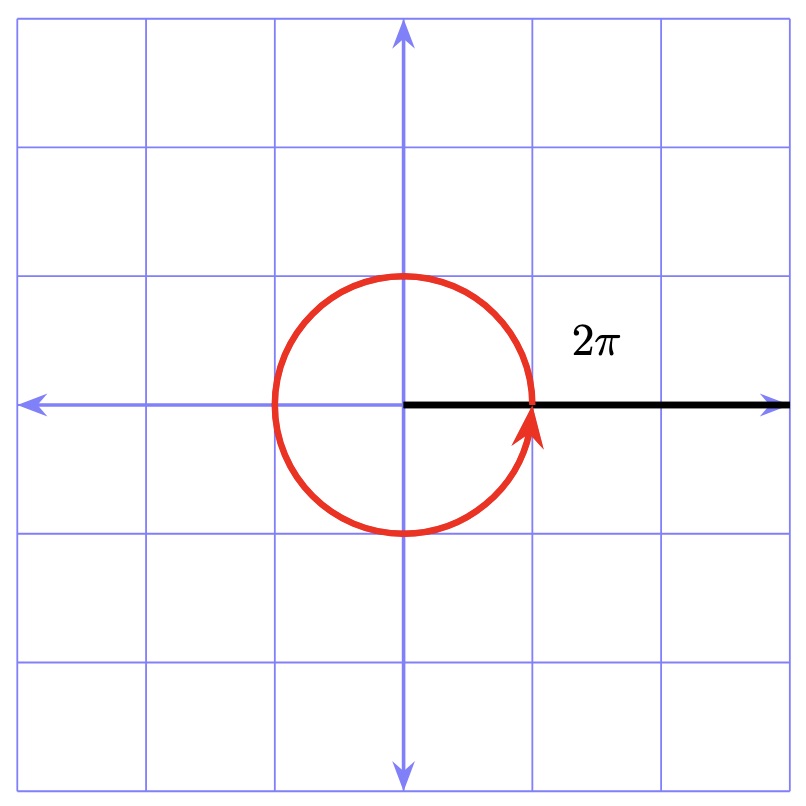
Pi can also be used to help measure angles. Instead of measuring angles with degrees, we can measure them with radians. Radians are another measurement of angle given in terms of pi. One radian is the angle we get from travelling the length of a radius around the circle. An image showing a measurement of one radian can be shown below.

A circle on a grid with an angle of one radian shown.