Parallel Lines and Curves

We can see parallel lines all around us, on radiators, railway tracks and pieces of paper. What properties do lines need to have to be parallel?

Parallel Lines

In short, parallel lines are lines that never cross. If two lines are straight, they can only be parallel if their gradients are equal. The gradient of a line describes how many units vertically a line moves over one horizontal unit. To read more about the gradients of straight lines, see our article on the properties of straight lines.

In the image below, we can see an example of two parallel straight lines, which have the same gradient. If we were to extend these lines forever, they would never cross.

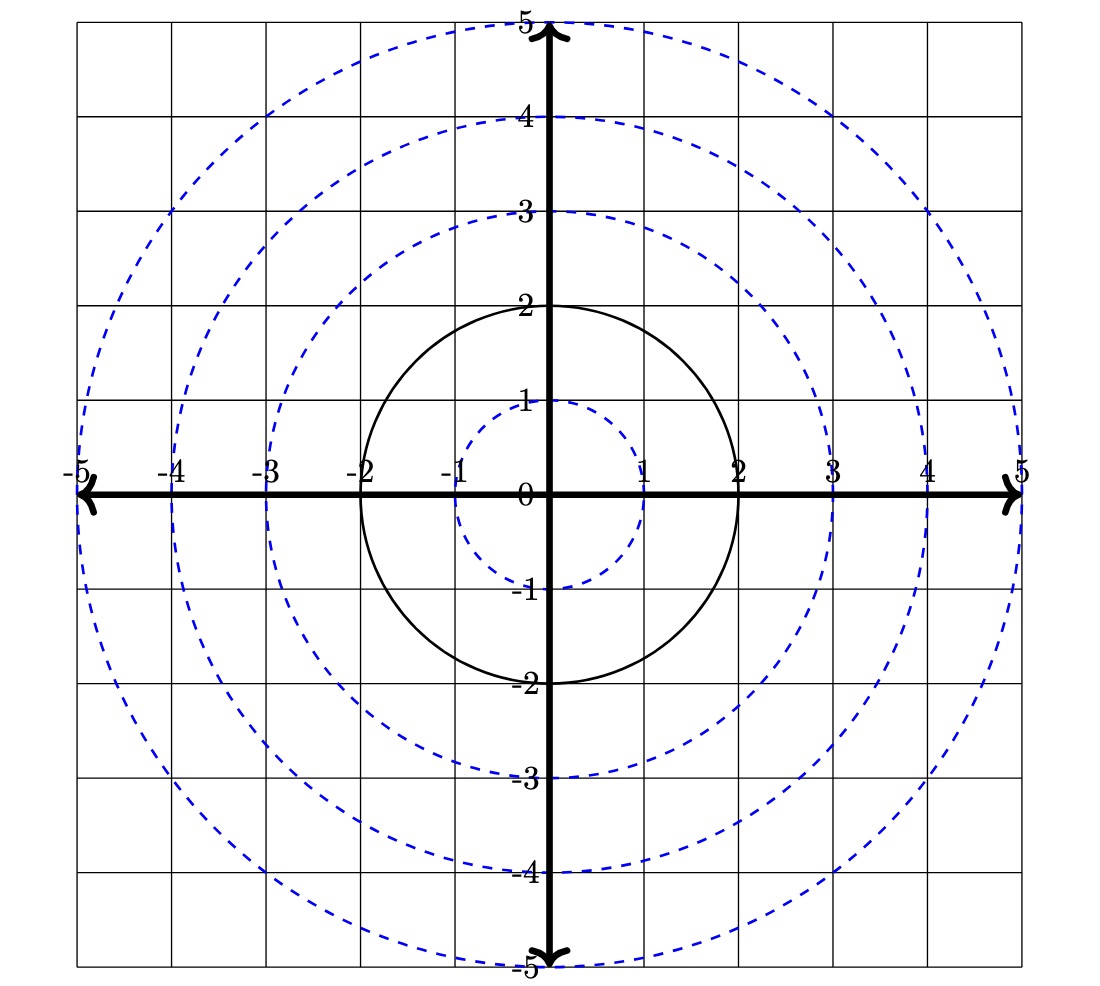
Parallel Curves

Lines that aren’t straight can also be parallel. Parallel curves are lines that are not straight but also never cross and maintain the same separation everywhere. We will not get too technical here, but discuss some examples children can explore.

A nice example of parallel curves is concentric circles, as shown in the image below. Another example children might be familiar with is drawings of rainbows.

Children can explore drawing parallel curves by keeping the distance between curves the same at all points. One way of finding these parallel curves is to use a compass to draw circles and then join up the furthest point on the edges of all the circles. In the image below, this technique has been used to find some parallel curves of the black shape.

Whilst a compass is sharp, and not appropriate in all settings, a similar effect can be achieved by tracing around a transparent circular object. Perhaps a lid, or a cardboard tube, could be used by children wanting to draw their own curves.

Another pair of lines that are defined by their gradient are perpendicular lines. To learn more about perpendicular lines, you can read our article on them.