Circles

Circles are a shape that is of particular interest to nursery school children, recurring in many discussions. The roundness of circles makes them ideal for use in toys and can lead to a lot of mathematical exploration. Below, we discuss some of the main features of circles and some practical activities children could try.

Centre

One key feature of a circle is its centre. Lying at the middle of the circle, all points of the circle are always the same distance from the centre. We can use this fact to help us draw circles, either by using a compass or by using a pin and string.

Children can experiment with drawing circles by fixing one end of a piece of string to a point. At a small scale, this could be done with a pin. On a larger scale, one child could stand holding one end of some string and another child could hold the other end of the string and walk around them, making a mark of where they walked with paint or some other medium. In both methods, by keeping an equal distance from the centre, the children can create a circle.

In the image below, we have drawn the centre of the circle in red. If we have a circle but have not been told where the centre is, we can find the centre in many ways; a couple of these are discussed later in this article.

Radius

The radius of a circle is a straight line that goes from the centre of the circle to the outer edge of the circle. As the edge of the circle is always the same distance from the centre, this line will always be the same length no matter which direction we draw it in.

In the image below, we have drawn a radius of the circle in red.

Diameter

The diameter of a circle is a straight line that passes through the centre of the circle and touches the edge of the circle on both sides. The diameter will be twice as long as the radius, as it is the same as two radii with the same gradient being joined together at the centre.

In the image below, we have drawn the diameter of the circle in red.

Circumference

The circumference of a circle is the name for the outer edge of the circle. The length of the circumference is determined by the length of the radius and the number \(\pi\) (pi). The length of the circumference is given by the equation: \begin{equation} \text{circumference} = 2 \times \pi \times \text{radius}. \end{equation}

If we double the length of the radius of the circle, the length of the circumference is doubled too. Children could experiment with this, using a measuring tape or a length of string to measure the circumference of the circle.

In the image below, we have drawn the circumference of the circle in red.

Tangent

We call a line tangent to a circle if it only touches the circle at exactly one point.

In the image below, we have drawn a tangent to the circle in red.

Chord

A chord is a straight line that is inside the circle with both of its endpoints touching the edges of the circle. The diameter is a special chord that passes through the centre.

In the image below, we have drawn a chord inside the circle in red.

Finding the Centre

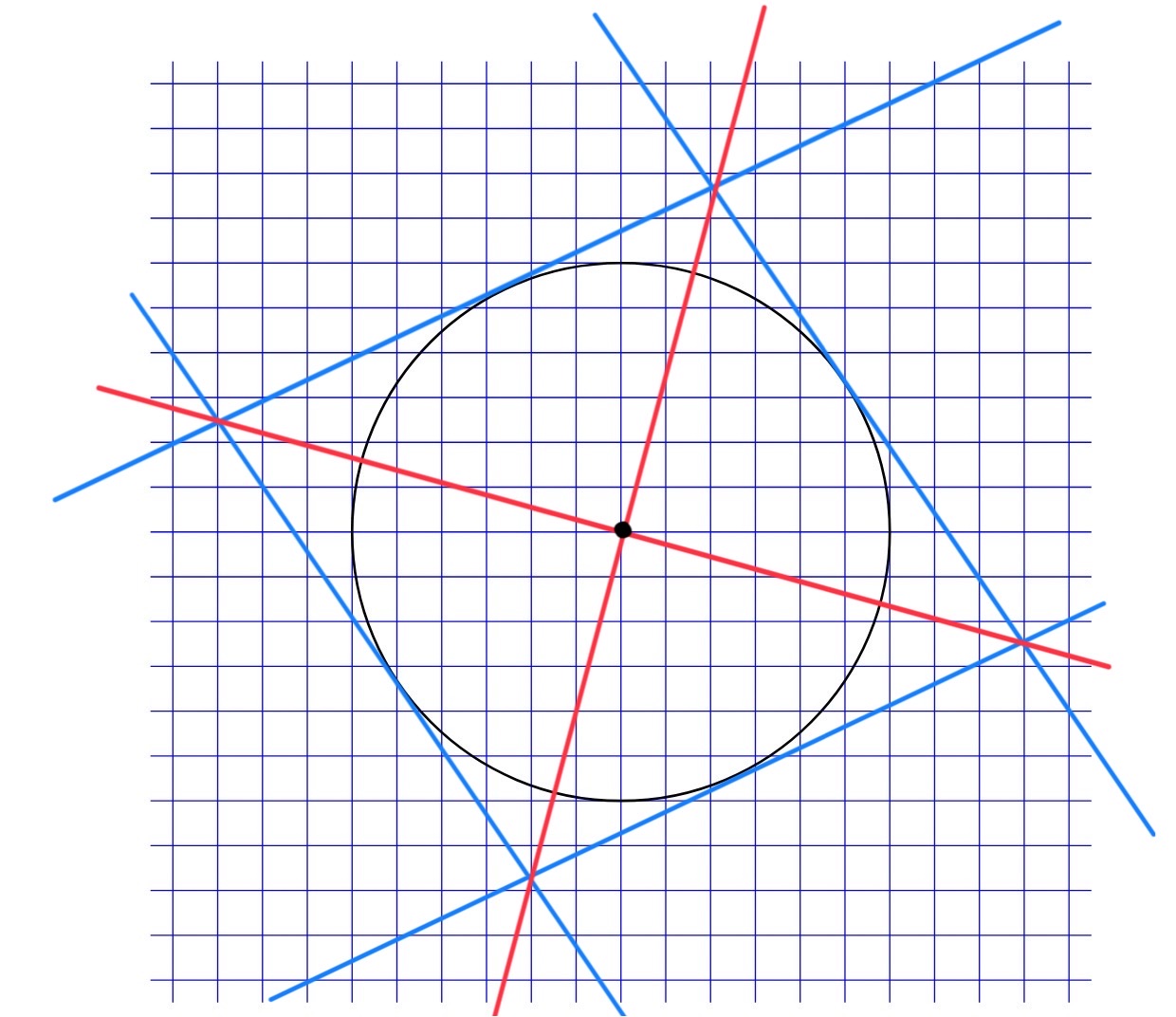
If we have a circle drawn on a piece of paper and want to find the centre, we could use parallel lines. First, we draw one tangent to the circle, then we draw another tangent parallel to this. We repeat this drawing another two parallel tangents, so that we have four lines in total. We then draw lines connecting the intersection points of the two sets of tangents. Where these two lines cross is the centre of the circle.

In the image below, this method has been used to find the centre of the circle.

In the image below, a child has used a string and this method to find the centre of a circle.

Another way to roughly find the centre of a paper circle could be to cut it out and use the centre of mass method to find the centre.

Area

The area of a circle is dependent on how large the radius is and the mathematical constant \(\pi\) (pi). We can calculate the area using the equation: \begin{equation} \text{area} = \pi \times \text{radius}^2. \end{equation}

Above, we saw that if we doubled the length of the radius, the circumference would also double in length. This is not the same case for the area in the equation above the length of the radius is squared. This means that the area of the circle will grow more quickly than the circumference as the length of the radius is increased. If the radius is doubled, the length of the circumference will double and the area of the circle will become \(4\) times bigger.

In the image below, we can see how the area of a circle increases as we double the length of the radius.

Equation

In a similar way to lines, circles can be mathematically described in a few ways, one is with a mathematical equation. Another way that is more accessible to young children is by giving three points that the circle passes through.

If we draw three points (that cannot be joined on one straight line), then there is a unique circle that connects these points. It can be a fun game for children to try and find the circle that connects all the points.

Stories About Circles

One famous mathematical story about circles is the story of the Queen of Dido. Dido was, according to old Greek accounts, the first queen of Carthage. She fled her home and asked for refuge in Northwest Africa. She asked for a bit of land that could be hers, and was allowed as much land as she could fit within an oxhide. She cleverly decided to cut the hide into thin strips and tie them together to make a large rope. With this done, she needed to determine the largest amount of land that could fit within the rope.

Trying to fit the largest amount of area inside a set amount of rope could be a fun activity that children could try in the classroom. They could use sand or different objects to fill the inside of the rope to compare the sizes of the area. They might be able to work out that the shape which contains the most area using the string is a circle. This is what Dido worked out.