Angles

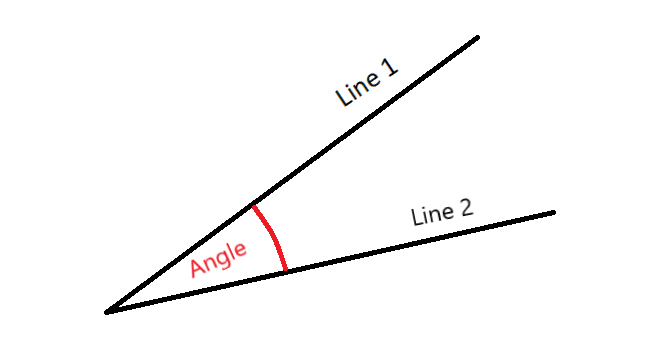
When two lines meet each other, they form an angle.

Children can use all sorts of materials to form angles…

“I will use my body. Look, me and E can do it! We are an angle, a right angle.”

The size of an angle is determined by how far around we have to go from one line to the other.

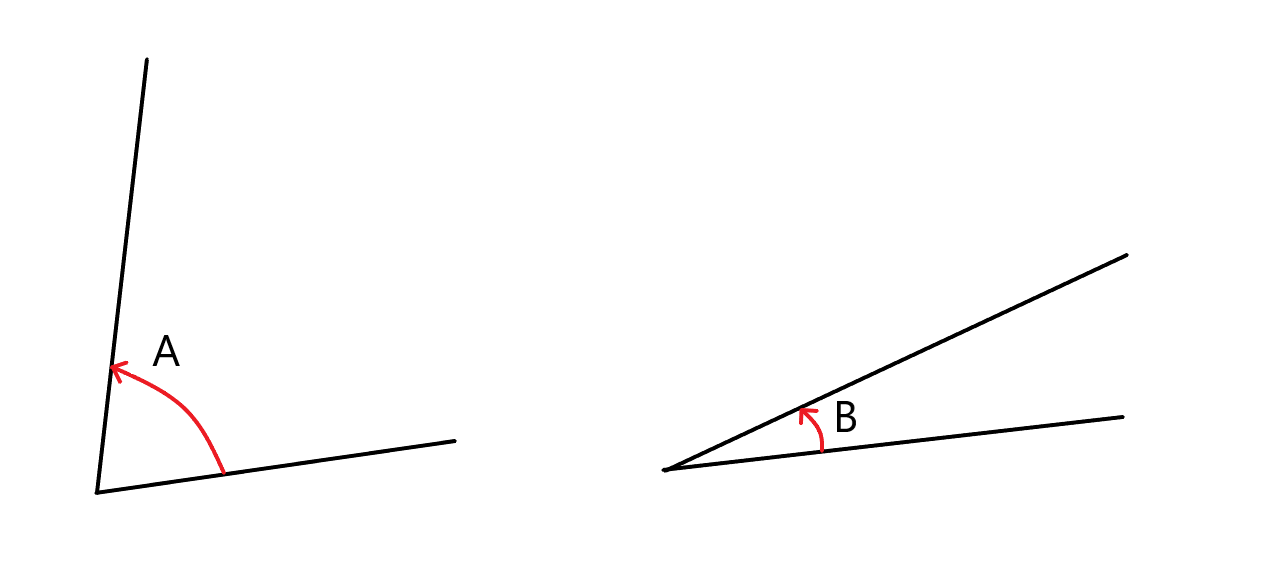
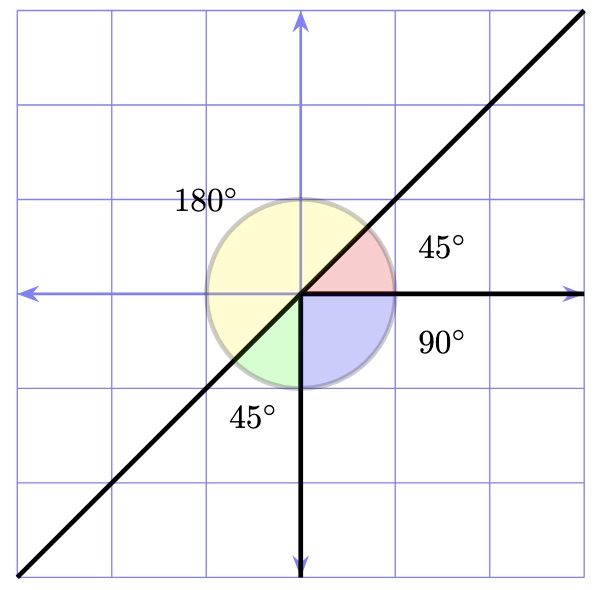
In the image above, angle A is bigger than angle B, because you have to go further round to get from one line to the other.

Engineers and scientists tend to measure angles in degrees, in which case there are 360 degrees all the way around the point. Mathematicians tend to use Radians, in which case there are \(2\pi\) (where \(\pi\) is the Greek letter ‘pi’, and represents the number 3.141592…).

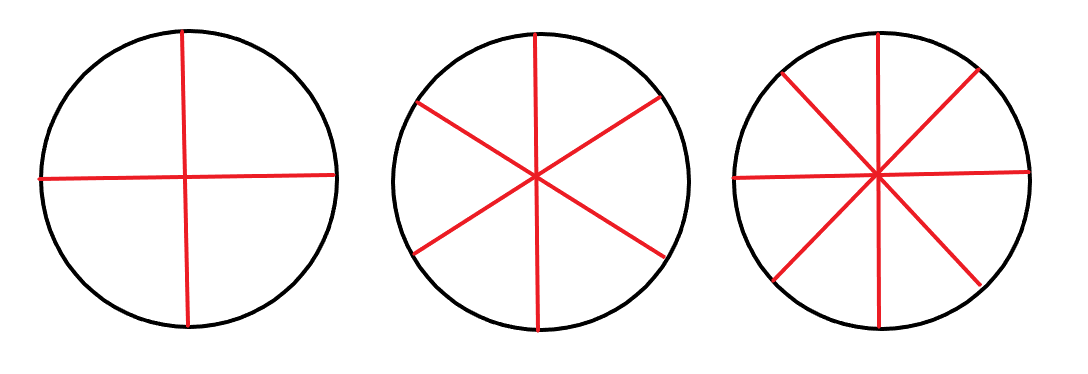
Neither of these measuring systems is very suitable for young children, since degrees involve very large numbers, and Radians involve strange decimal numbers (like \(\pi\)). One way that is simpler is to think of ‘how many of this angle fit into a circle?’.

In the picture above, the left-most diagram shows the largest angle; only four will fit into a circle. The angle in the middle diagram is slightly smaller, and six will fit together. The angle to the right is smaller still, with eight filling the circle.

If the angle is occurring somewhere real, there might not be an actual circle to fill, but still the angle can be thought of in this way.

One source of confusion was whether the length of the lines (or ‘legs’) had anything to do with the size of the angle. It doesn’t! One way to demonstrate this is with objects that create a changing angle (but with lines that don’t change length). Examples include scissors, books, doors, or even just pieces of folded carboard.