Spirals

An interesting shape that occurs in nature is the spiral. Children can find spirals all around them, on the shells of snails, in flowers and animal horns. There are many types of spirals, which are defined by different mathematical equations; a few key examples of spirals are given below. Knowing the names of the spirals can be nice, but it is more interesting to think about how the spirals look different.

Archimedean Spirals

These spirals are evenly spaced, meaning that children can sketch them by keeping their pencil the same distance from the line at all times as they spiral around. We can continue to draw this spiral until it reaches the edge of the paper. An image of the Archimedean spiral is shown below.

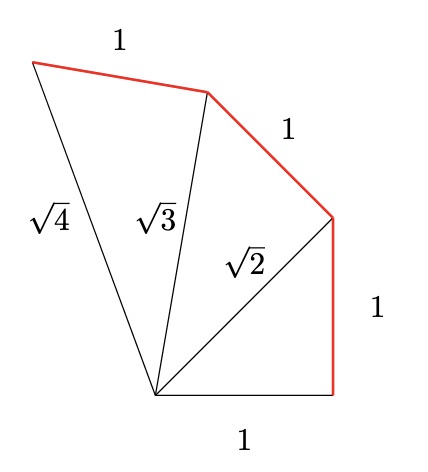
We can approximate an Archimedean spiral using triangles; this is called the Spiral of Theodorus and is shown in the image below. Each triangle is a right-angled triangle with one side having a length of \(1\). The first triangle has the other two sides of length \(1\) and \(\sqrt{2}\), the second triangle has the other two sides being \(\sqrt{2}\) and \(\sqrt{3}\). Essentially, the triangles increase in size and stack together to form this spiral. The most interesting takeaway from this is that children can experiment with making spirals using triangles.

Fermat spirals

A type of spiral that gets tighter as we move away from the centre is a Fermat spiral, which can be seen in the image below. Fermat spirals can sometimes be seen in the arrangement of leaves and seeds in plants.

If we zoom in on the centre of the sunflower, we can see the spiral pattern.

In the image below we can see children exploring the spirals in pinecones.

Logarithmic spirals

These spirals become more spread out the further out you go. This type of spiral is self-similar in a similar way to fractals. If you looked at a section of a logarithmic spiral, it would have the same shape as another section of the spiral. If you haven’t read our article on fractals yet, check it out!

These types of spirals are common in nature, and one special case of this is the Golden spiral. An example of a logarithmic spiral is shown in the image below.

One example of logarithmic spirals in nature is snail shells, as shown in the image below.

The Golden Spiral

The golden spiral is a special type of logarithmic spiral where specific values are used in the underlying mathematical expression. We can draw our own approximation of the golden spiral using the Fibonacci numbers as shown in the diagram below. The Fibonacci numbers are a famous sequence of numbers that often occur in nature. See our article on the Fibonacci numbers for more information. The first Fibonacci numbers are \(0,1,1,2,3,5,8,13,21,34,...\).

If we draw two squares with side length \(1\) on top of each other, we can then begin constructing our spiral. We draw a square with a side length of \(2\) next to our first two squares and then continue in this way, adding squares with side lengths \(3,5,8,13\) and so on. If we then add a quarter circle in each square, we get an approximation of the golden spiral, as shown in the image below.