Properties of Straight Lines

There are straight lines all around us, but how can we describe them mathematically? This is an important question if we want to compare the lines that we see around us.

Every straight line can be determined by two points. If you draw two points on a piece of paper, there is a unique straight line that passes through them. This is a fun doodling game that children can try. First, they can draw the points, and they can use a straight edge (such as a ruler) to find the straight line that passes through the two points.

How else can we define a line? When describing a straight line mathematically, we normally use an equation; this serves the same purpose as writing down the two points that the line passes through. By describing the line as an equation, we can encode more information about how the line behaves.

The equation of a line can be given in a few forms, but the most common is: \begin{equation} y=mx+c. \end{equation} Here $m$ tells us the gradient of the line and $c$ tells us the intercept of the line.

The Gradient

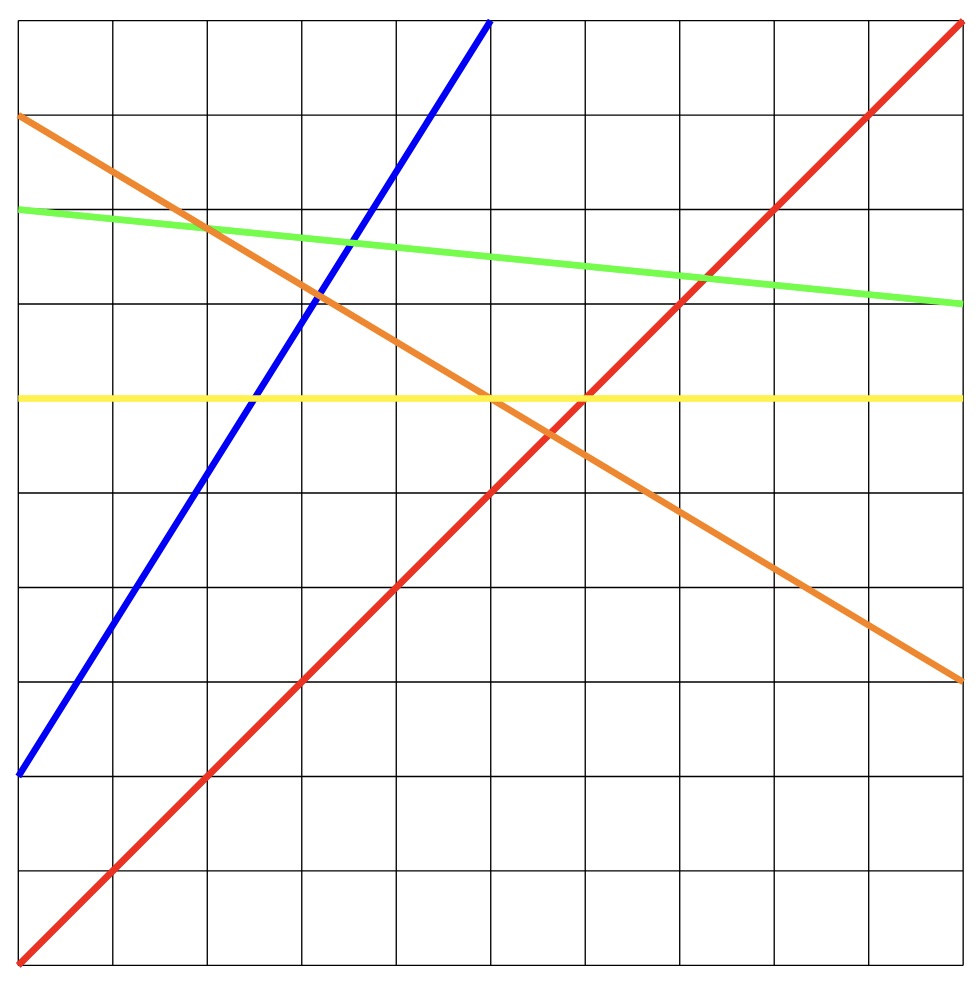
The gradient of a line describes which way the line travels. Does the line go up or down (as we look from left to right)? There are a few examples of lines in the image below. A line with a positive gradient goes up as we look from left to right. A line with a negative gradient goes down as we look from left to right. A line with a gradient of zero is flat, not going up or down as we look from left to right.

In the image below, we can see that the red and blue lines have positive gradients, the green and orange lines have negative gradients, and the yellow line has a gradient of $0$.

Straight lines with different gradients.

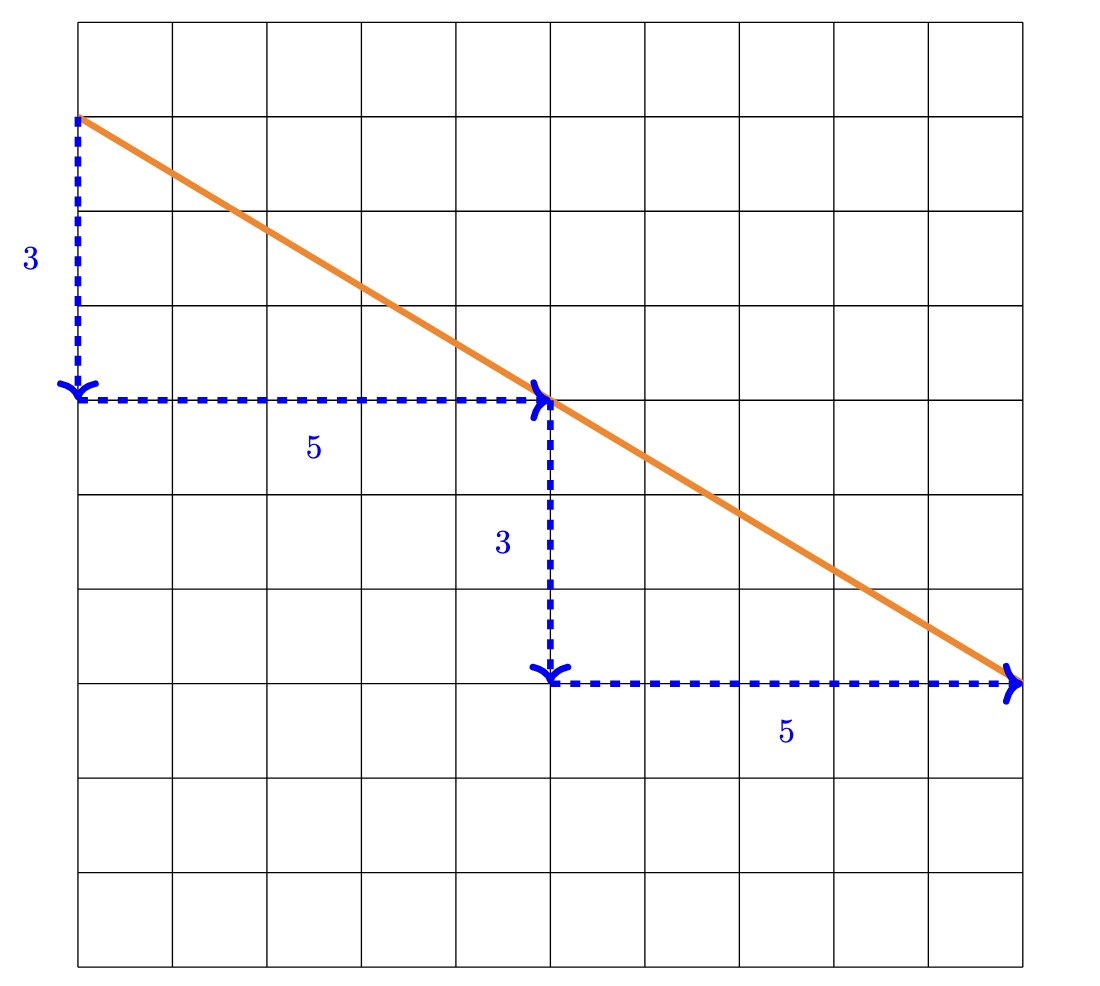
We can calculate the gradient by comparing how many units up (or down) a line goes for each unit along. In the image below, we see that the orange line goes down by $3$ units for every $5$ units along. This means that for each unit along, the line moves down by $\frac{3}{5}$ units. The gradient of the orange line is then $-\frac{3}{5}$, there is a negative sign as the line moves downwards as we move to the right.

An example of calculating the gradient of a line.

The Intercept

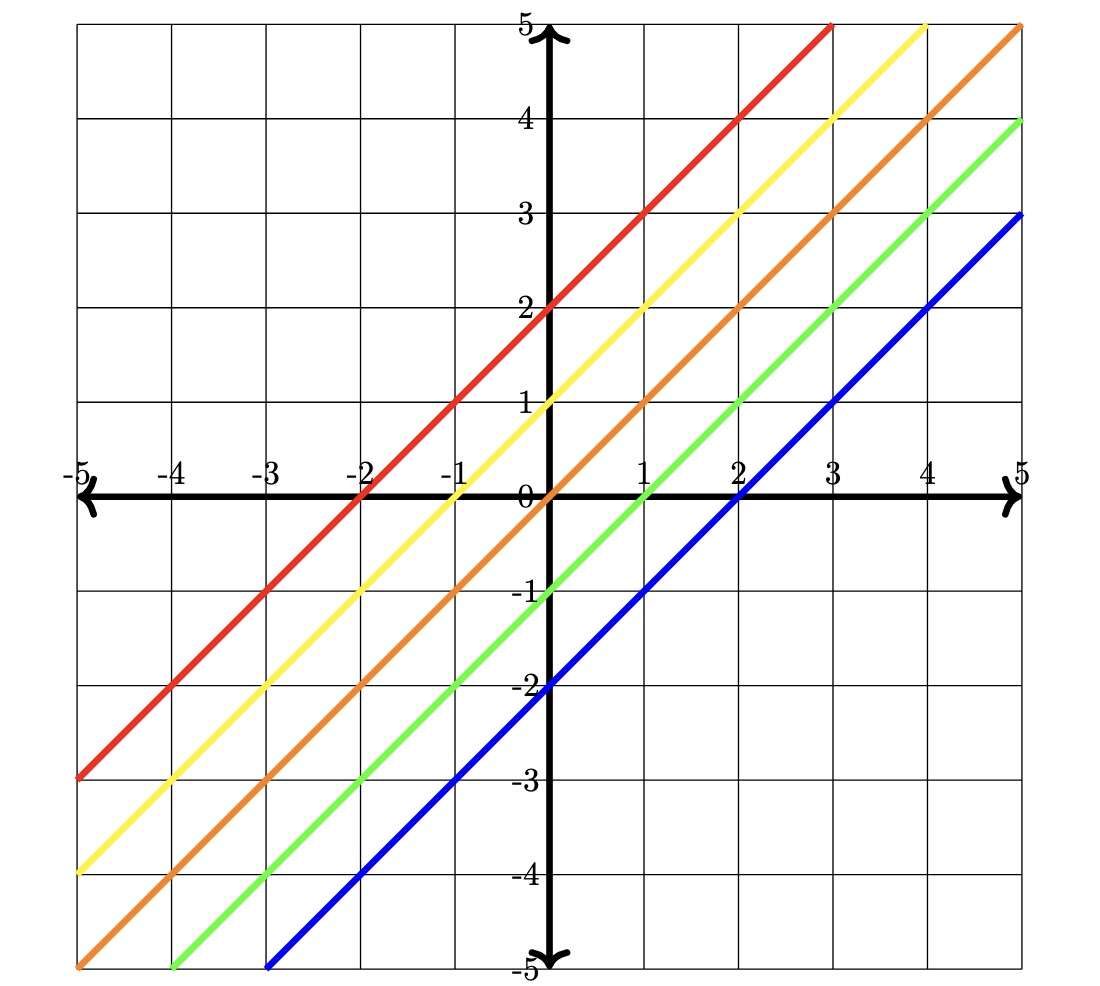
The intercept of a line describes its position. If we think about the position of straight lines with respect to some axis (as shown in the image below), we can describe where each of the straight lines intersects the vertical axis (this is normally called the y-axis).

In the image below, we can see an example of lines with the same gradient but with different intercepts.

An example of lines with the same gradients and different intercepts.

The Equation of a Line

Once we know the gradient and intercept of a line, we can then write the line using the equation \begin{equation} y=mx+c. \end{equation}

In the image below, we can see that the line has a gradient of $-\frac{3}{5}$ and an intercept of $1$, meaning we can write the line as $y = -\frac{3}{5}x + 1$.