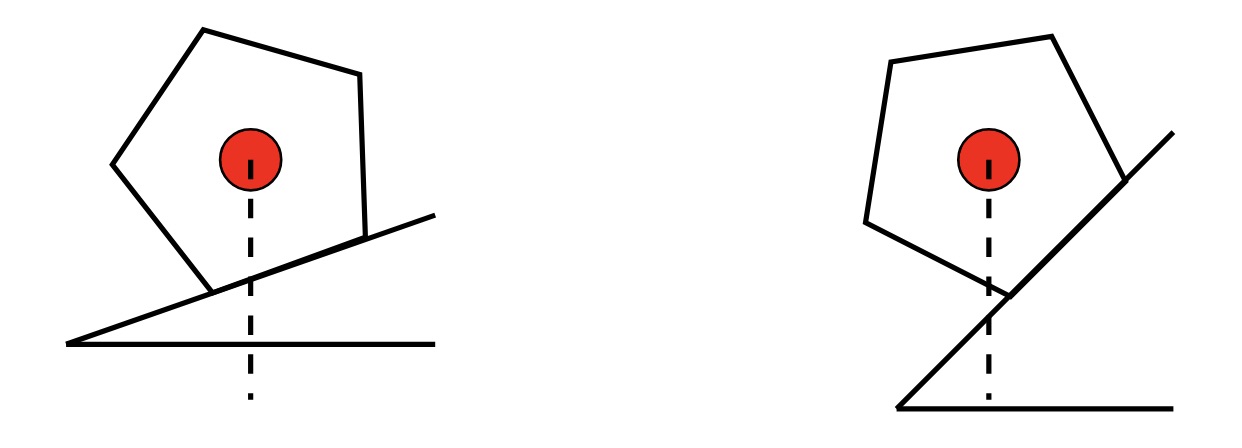Centre of Mass

A common playtime activity is stacking blocks. Most of the time, children want to build the tallest towers, which leads them to question how to make their tower taller. To make the towers taller, the biggest problem is usually stability. How can they make their towers more stable?

One way of making a tower more stable is by using a larger base. Why does this work? Making the base of the tower larger means that the centre of mass of the tower can move further. A tower will topple if the centre of mass of the tower is not over the base.

Mass is a word we use to describe the material of an object. The words mass and weight are often used interchangeably, even though they have slightly different scientific meanings.

The centre of mass is the point where we model all of the mass of an object to act from. Looking around the classroom, children can find many objects with a wide base. If some of these objects were flipped upside down, they might not balance.

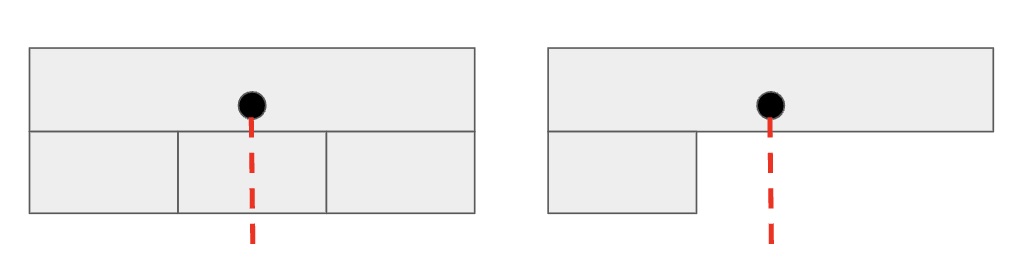
If we think about a game of Jenga, we can see how the centre of mass affects the stability of the tower. On the left-hand side of the diagram below, we can see how the centre of mass of the top Jenga block is above the base of the tower. On the right-hand side of the diagram, we can see that the centre of mass of the top Jenga block is not above the base of the tower; this would mean that this top Jenga block would fall off the base. Here we have only looked at the centre of mass for the top block of the tower, not the whole tower. Finding the centre of mass for the tower would require some more complex geometry, which is not necessary for this discussion.

Two Jenga towers with different base sizes.

In the images below we can see some examples of towers that children have built. One child said “The blocks have to be in the middle and they don’t tip over”.

A mathematical problem involving stacking blocks is called the Leaning Tower of Lire and was discussed by Paul Johnson in 1950. He wanted to learn about how far the top block could be pushed from a stack of blocks to create an overhang before the tower toppled.

We can see lots of examples of wide bases in architecture. The shard has a much wider base and then gets thinner as its height increases. An example of this is shown in the image below.

The Angel of the North has wings which are much wider than its base. To ensure stability, the structure has a large weight embedded below ground level. This weight changes both the centre of mass (by bringing it lower) and the base by making it wider and supported by the ground on multiple sides.

A toy that showcases the use of the centre of mass is the balancing bird; this bird can balance perfectly on the point of its beak. Below is a picture of this balancing bird made from paper. The mass in the wings and body of the bird is evenly distributed, meaning the centre of mass of the bird is at the beak, and the bird can balance here.

An origami bird balancing on its beak, on the top of a pen.

A fun activity for children to try is finding the centre of mass of a 2D shape. This can be done using a pin and a string with a weight (a plumb line). Some images of this process are below. Pin the object at different points around its edge (making sure the object can turn freely) and record the plumb line on the object. The centre of mass is where all the plumb lines cross. We only need two lines to find the centre of mass, but we use more to account for error.

Demonstration of finding the centre of mass of a 2D object.

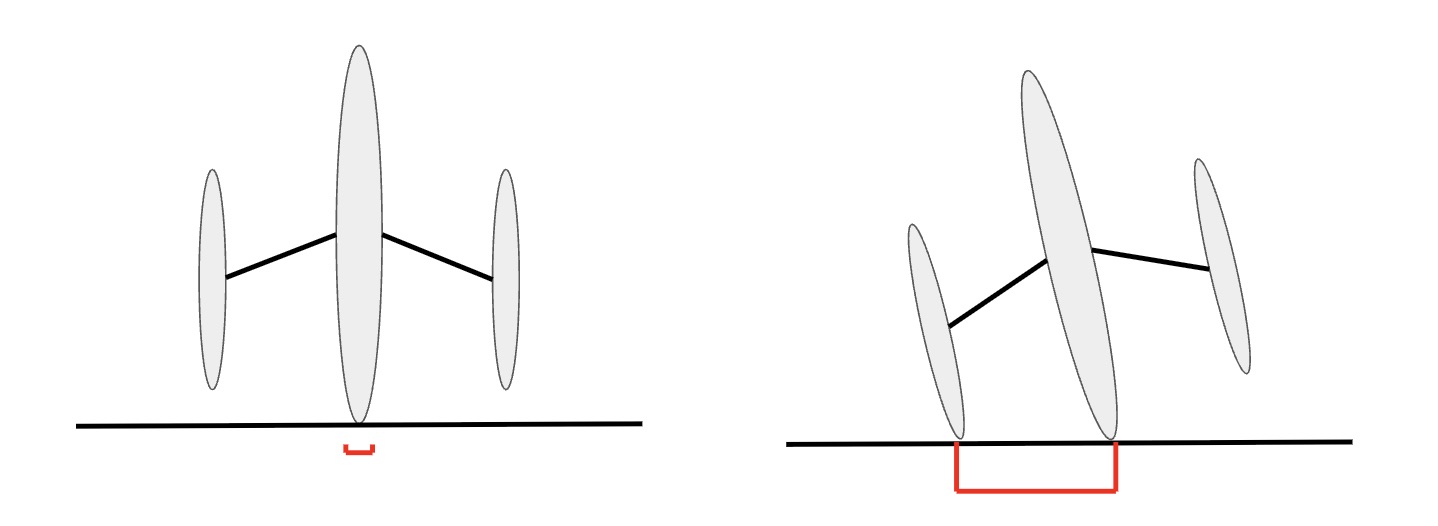
There are many examples of making things more stable by increasing the base size, for instance, stabilisers on bikes. Whilst the stabilisers should not touch the ground when the bike is balanced perfectly upright, they will when the bike begins to lean. This extra contact point widens the base of the bike, meaning it stays upright. In the image below, we can see the difference in the base size when the stabiliser comes in contact with the ground.

Two diagrams of the wheels of a bike with stabilisers, in the right hand diagram the stabiliser is in contact with the ground widening the base of the bike.

The position of the centre of mass is also important when rolling objects on ramps. In the diagrams below, we can see that the pentagon will only roll down the ramp when the ramp is steep enough. The ramp needs to be steep enough that the centre of mass is not above the base of the pentagon, as shown on the right-hand side of the diagram. Children can experiment with this using pencils on a cardboard ramp, increasing the angle of the cardboard until the pencil rolls.

Two diagrams of pentagons on ramps, the ramp on the right is steeper. Vertical dotted lines show that the centre of mass of the pentagon on the steeper slope will fall outside of the base.

As we increase the number of sides the polygon has, the centre of mass no longer lies above the base. As the number of sides of the polygon tends to infinity, our polygon approximates a circle, which will roll on any non-flat ramp. A circle has a base of a single point, and so the centre of mass is not above the base unless the ramp is perfectly flat.

In the image below, we can see how shapes with fewer sides will not roll on the ramp, but shapes with more sides will.