Angles in Shapes
In shapes, we can see lots of different angles. How can we compare these angles? Here we will think about interior angles in polygons. Polygons are 2D shapes with straight lines, such as hexagons.
The interior angles of a polygon are the angles inside the shape. An example of an interior angle in a hexagon is shown in the image below.
The interior angles of a polygon will always add up to \((n-2)\times180\) degrees, where \(n\) is the number of sides the polygon has. This means that the more corners a shape has, the larger the total number of degrees inside the shape.
In a regular polygon, all the sides are the same length, and the angles in each of the corners are the same size. Irregular polygons have varying angles and side lengths. The sum of the interior angles will be the same regardless of whether the polygon is regular or irregular. An example of an irregular hexagon is shown in the image below.
The size of each of the angles in a regular polygon is given by \((1-\frac{2}{n})\times180\) when \(n\) is the number of sides. This means that as the number of sides gets larger, the angle inside the shape gets larger and closer to \(180\) degrees. If you have read our article on angles, then you might remember that \(180\) degrees is a flat line. This means that as the number of sides in a polygon increases, the angles inside the polygon look more like a straight line.
In the table below, we can see that as we increase the number of sides a regular polygon has, the size of each interior angle approaches \(180\) degrees.
| Number of Sides | Sum of Interior Angles | Size of Each Angle |
|---|---|---|
| \(3\) | \(180^\circ\) | \(60^\circ\) |
| \(4\) | \(360^\circ\) | \(90^\circ\) |
| \(5\) | \(540^\circ\) | \(108^\circ\) |
| \(6\) | \(720^\circ\) | \(120^\circ\) |
| \(7\) | \(900^\circ\) | \(128.6^\circ\) |
| \(8\) | \(1080^\circ\) | \(135^\circ\) |
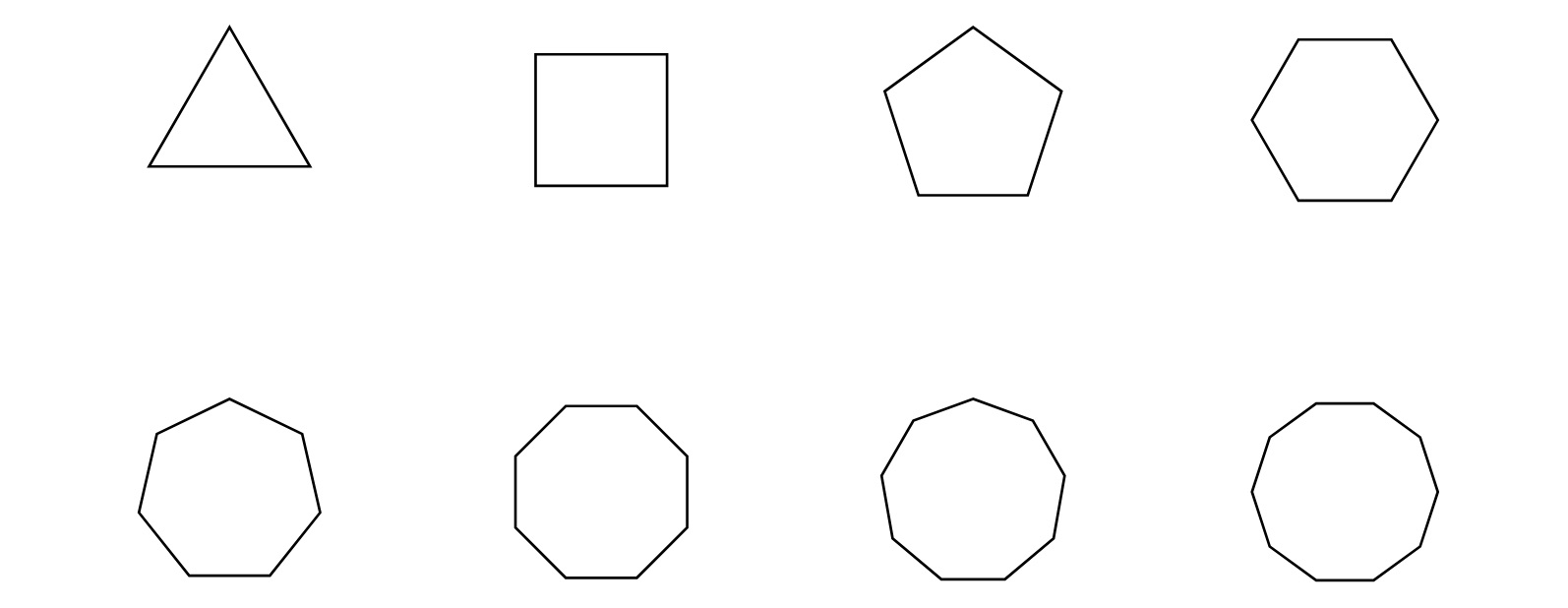
Children may be able to notice that for polygons with a small number of sides, there is a greater change in the size of the interior angles when we add an extra side than when we had a large number of sides to start with. For example, a square and a triangle have a large difference in their interior angles (\(30^\circ\)) and look very different. An octagon and heptagon, however, have a much smaller difference in the size of their angles (less than \(7^\circ\)) and look a lot more similar. The children might be interested in this pattern where the change between each shape seems smaller and smaller as the number of sides increases.
In the image below, we can see polygons with a differing number of sides, from \(3\) up to \(8\). In this image, we can see that the heptagon and octagon look quite similar, whereas the triangle and the square look quite different.