The Four Colour Theorem

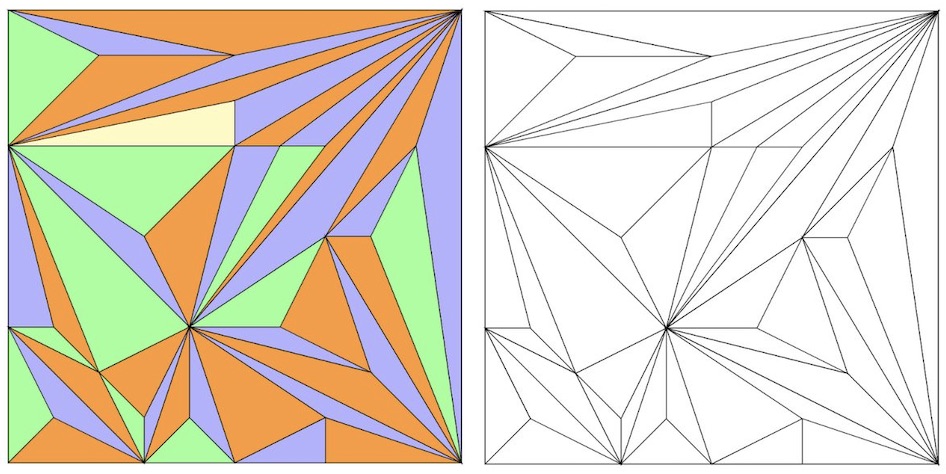
One popular classroom activity is colouring, and an interesting mathematical property is the four colour theorem. If we have at least four colours, we can fill in a drawing or map so that no sections that are next to each other (share an edge) are the same colour. We call sections that share an edge adjacent. In the images below, we can see that the drawing has been coloured in using four colours, and no adjacent sections are the same colour. We are not worried about sections that meet at a point here. You can try the colouring yourself by printing a copy of the blank image, or you could try with a picture of your own.

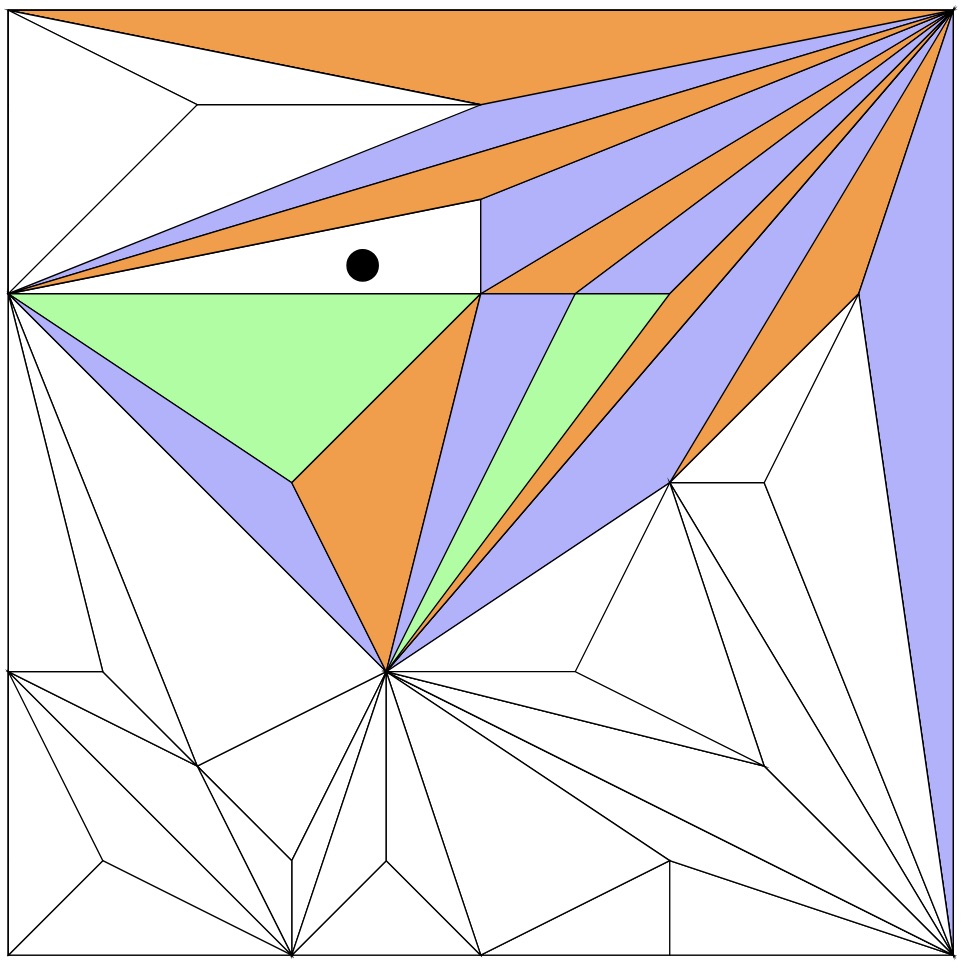
It is not possible to colour this image so that no adjacent sections are the same colour when we only have three colours. In the image below, we can see that when we only have three colours, we run into a problem with the section containing the dot. We can not colour this section orange, purple or green without two sections of the same colour being next to each other.

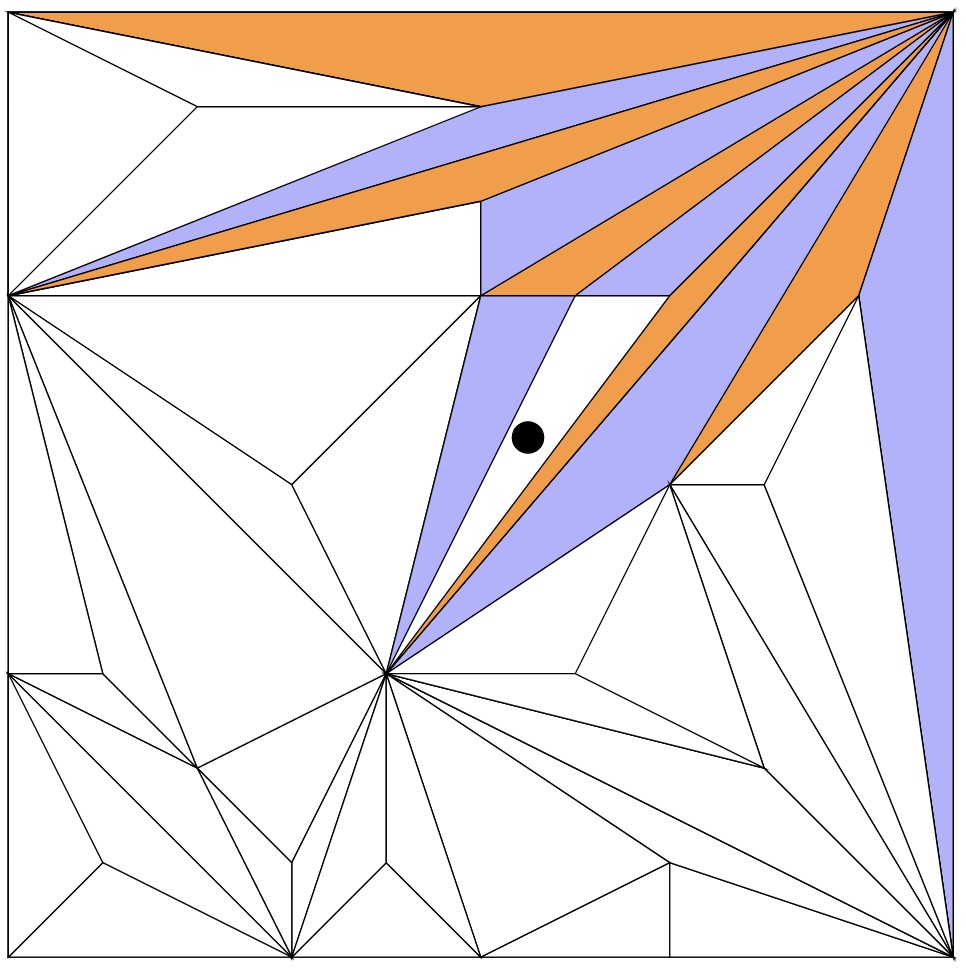
When we only have two colours, we run into problems even sooner. In the image below, we see that we cannot colour the section containing a dot orange or purple without two sections of the same colour being next to each other.

Colouring problems like this are fun for children to attempt, and they can also start discussions about the best strategies. For instance, it is logical to start with one of the triangles in the image and then work your way around the image by colouring the next adjacent triangles. If we started by colouring triangles in different corners of the drawing, we might not be able to find a way to colour in the drawing correctly with only four colours. Children could develop their own strategies for tackling the problem and talk about why they are effective.