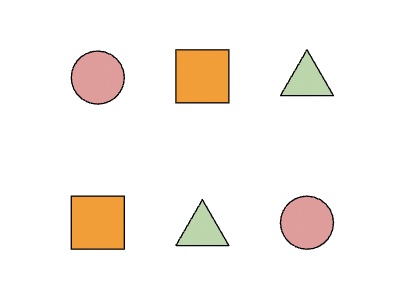Permutations
Many children are interested in ordering objects by size or some other property; this can lead to a discussion about permutations. A permutation is a reordering of a group of objects. This can be explored using items around the classroom or by the children organising themselves in a line. In the image below, we can see that the original order of the objects has been rearranged to give another permutation of the objects.
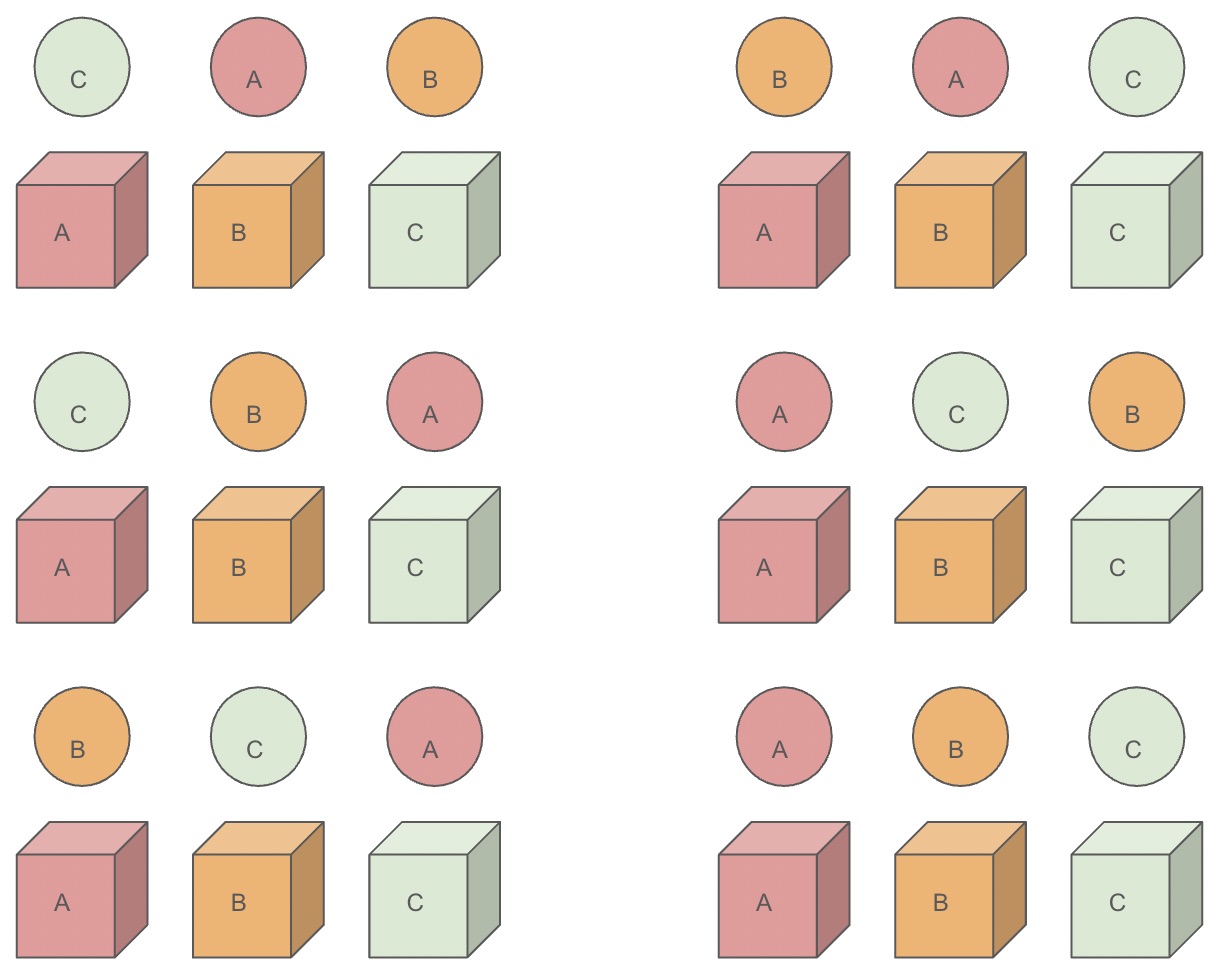
Sometimes it can be useful to know how many ways there are to arrange a group of objects. For a small number of objects, the children can find all possible rearrangements. In the image below, we see all \(6\) permutations of the \(3\) objects.
Rearrangements of objects also occur in children’s books. In the story of Goldilocks and the three bears, each bear has its own special chair. It might be interesting to think about the number of ways the bears could sit in the different chairs. If we think of the chairs being fixed in a certain order on the floor (the bears can move but the chairs cannot), there is only one order the bears can sit in so that they are all in their own chairs. This is similar to the permutations explored above, and we can see the different permutations of the bears in the following image, where the bears are represented by the circles and their chairs by the cubes (chair A belongs to bear A). In the image, we can see that all the bears will only be happily in their own chairs in the bottom right permutation.
Questions that children may ask could include, what happens when there are a different number of objects? When there is only \(1\) object, there can only be one arrangement and for \(2\) objects, it is easy for the children to find the \(2\) possible permutations. When there are more than \(3\) objects, the number of permutations grows quickly, and it could be interesting to talk about how adding a fourth object creates \(4\) times as many permutations. The number of permutations for up to \(6\) objects is shown in the table below.
| Number of Objects | Number of Permutations/Orderings |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |