Numicon
Numicon is a great resource, allowing children to learn about the partitions of different numbers. Numicon are tiles representing the numbers \(1\) to \(10\) and can be stacked on top of each other. In the image below, we can see a child comparing two tiles made of \(3\) squares to one tile made of \(6\) squares. “Four ones is equals four”, “two ones equals two”, “three plus three is six” are some of the observations that the child made with the help of a nursery practitioner.
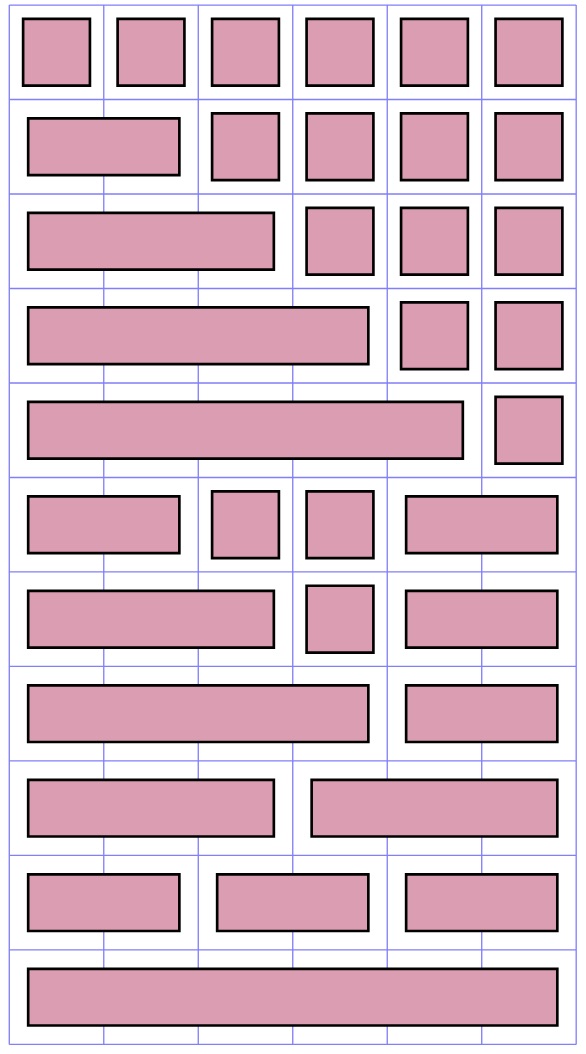
Here, the child has explored one partition of the number \(6\). The number \(6\) has eleven partitions, which are represented in the image below.
It could be a fun activity for children to try to find the partitions of numbers for themselves. In the table below, the number of partitions for the numbers \(1\) to \(10\) are given, these get large quite quickly.
| Number | Number of partitions |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 5 |
| 5 | 7 |
| 6 | 11 |
| 7 | 15 |
| 8 | 22 |
| 9 | 30 |
| 10 | 42 |
By its modular nature, Numicon can also be used to make patterns, the same child used Numicon to recreate a pattern. This sparked a conversation about how to orient shapes with the practitioner. As some of the blocks can be placed in two distinct ways on the grid, this meant that the terminology of horizontal and vertical could be used. When recreating the pattern, the child said, “the blue one is ten, I need to put it near non four.” “Non four” refers to a blank space of size four. Here, by trying to make a pattern, lots of mathematical vocabulary and reasoning is being used.
This resource could also be useful for exploring multiplication by having multiple copies of the numicon blocks, the children might be able to see that five lots of the four numicon blocks sum to twenty.
Numicon is designed so that children can easily make pairs of numbers sum to ten. Pairs summing to the same number is a useful feature to be able to identify. There is a famous story about how the mathematician Gauss impressed his teacher by very quickly adding together every digit from \(1\) to \(100\). Gauss was able to do this so quickly as he recognised the importance of number pairs. He realised that by pairing numbers together (\(1\) with \(100\), \(2\) with \(99\)) the sum became \(101 \times 50 = 5050\).