Eggs and Spaces

One child was interested in plastic egg shells and placing each half in a spot in an egg carton. They grouped the egg shells by size, letting the larger ones take up more space in the carton. This can be seen in the image below.

Two egg boxes, each with some plastic egg shells sitting in the holes

This is a good activity in spatial reasoning and comparison, and could be developed further by asking the question, how many eggs do we need to fill the carton?

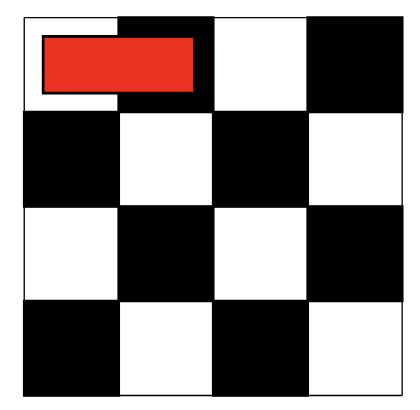
This is related to a mathematical problem called dominoes on a chessboard. This puzzle asks that for a given chessboard, i.e. \(4\times4\) is there a way of covering every square with dominoes such that each domino covers exactly one square of each colour on the board. An example of an allowed move is shown below.

A red domino covering a white and black square on a four by four chess board.

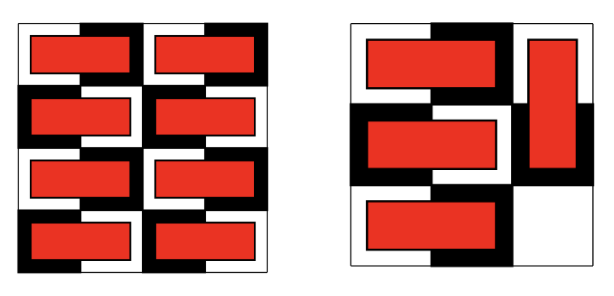
We can do this on the 4 by 4 chessboard, but we can’t do this on the 3 by 3, as there is an odd number of squares. As there are more white than black squares on the 3 by 3 chessboard, the square that is left over is white. We can see this in the image below.

A four by four and a three by three chessboard covered in red dominoes. The three by three chessboard has a white square that can’t be covered.

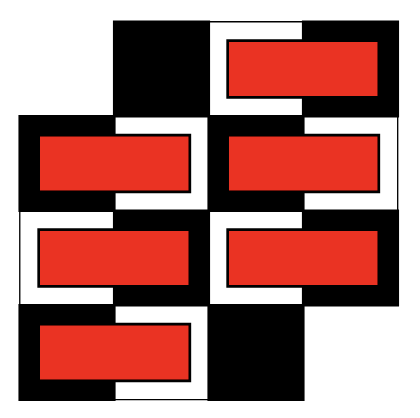
To cover every square on the board with a domino, we not only need an even number of squares but equal amounts of each colour. If we took opposite corners of the 4 by 4 chessboard away, we could no longer cover every square with a domino, even though we would still have an even number of squares. This is because we would not have an equal number of black and white squares. This is shown in the image below.

A four by four chessboard missing opposite corners (both of which were originally white), nearly covered in red dominoes.

This is similar to filling the egg cartons as the child will have to think about the total number of squares. Each half of the egg will take up one spot in the carton, meaning the components of the whole egg take up two spaces in total. Dominos on a chessboard, however, adds an extra layer of complexity by forcing further restrictions on where we can place the dominoes.